Large Numbers
First page . . . Back to page 5 . . . Forward to page 7 . . . Last page (page 11)
Graham's Number, and Famous non-Graham Numbers
We now discuss "Graham's Number", in quotes because there are at least three different versions, summarized by this table.
|
All of these numbers are variants of the same method of recursive hyper() function evaluation, and the concept of "Graham's number" is probably more strongly associated with this type of iteration than with any of the specific exact numbers that carry the name.
This recursive application of the hyper() function to itself is called "expansion" or "expandal growth" by the googology community. The most important parameter in an expansion is the number of "rows" above, which is the number of times hyper() is iterated. As we will see, expandal growth with n rows is comparable to the value of fω+1(n) in the fast-growing hierarchy.
The "Graham-Rothschild Number"
The original genuine "Graham's number", from a 1971 paper by Graham and Rothschild [40], is an upper bound for a problem in Ramsey theory, (graph colouring, combinatorics).
The problem is to determine the lowest dimension of a hypercube such that if the lines joining all pairs of corners are two-coloured, a planar graph K4 of one colour will be forced. "All pairs of corners" means that there are lines on every diagonal of the hypercubs, i.e. about 22d lines for a d-dimensional hypercube. K4 is a totally-connected graph with 4 edges, topologically equivalent to the 4 vertices and 6 edges of a tetrahedron. The planar requirement means that its 4 vertices are in one plane, meaning that it can't be just any 4 vertices of the hypercube, but diagonal planes are okay. (See the article by Sbiis Saibian40 [63] for an extremely thorough description with lots of illustrations.)
In 1971 Graham and Rothschild proved that an answer exists using an upper bound F(F(F(F(F(F(F(12,3),3),3),3),3),3),3), where F(m,n) is defined:
F(m,n) = { 2^n for m=1, n>=2 { { 4 for m>=1, n=2 { { F(m-1,F(m,n-1)) for m>=2, n>=3
 Graham and Gardner's 1971 description of the number |
Some work is needed to see how F(m,n) can be expressed in terms of hy(a,b,c). Let's start with F(2,n):
F(2,1) is not defined F(2,2) = 4 = 2^2 F(2,3) = F(1,F(2,2)) = 2^F(2,2) = 2^2^2 = hy(2,4,3) F(2,4) = F(1,F(2,3)) = 2^F(2,3) = 2^2^2^2 = hy(2,4,4) F(2,5) = F(1,F(2,4)) = 2^F(2,4) = 2^2^2^2^2 = hy(2,4,5) F(2,n) = hy(2,4,n) = 2^^nWith this general formula for F(2,n) we can proceed to F(3,n):
F(3,1) again is not defined F(3,2) = 4 = 2^2 = 2^^2 = hy(2,5,2) F(3,3) = F(2,F(3,2)) = 2^^F(3,2) = 2^^2^^2 = hy(2,5,3) F(3,4) = F(2,F(3,3)) = 2^^F(3,3) = 2^^2^^2^^2 = hy(2,5,4) F(3,n) = hy(2,5,n) = 2^^^nNow we have a F(3,n) formula, and the same sort of derivation shows that F(4,n) = hy(2,6,n), and so on, so in general
F(m,n) = hy(2,m+2,n)Now we can define a function lgn(n) (lgn stands for "lesser Graham number") for various numbers of nested F(F(F(...))) in the original text. For n=1 we'll define it in terms of the generalised hyper function.
lgn(n) = { hy(2,14,3) for n = 1 { { hy(2, lgn(n-1), 3) for n > 1Using this, F(F(F(F(F(F(F(12,3),3),3),3),3),3),3) is equal to lgn(7). In other words, using up-arrows:
lgn(1) = 2↑↑↑↑↑↑↑↑↑↑↑↑3 (12 up-arrows)
= hy(2, 14, 3)
lgn(2) = 2↑↑↑...↑↑↑3 (with lgn(1) up-arrows)
lgn(3) = 2↑↑↑...↑↑↑3 (with lgn(2) up-arrows)
. . .
lgn(7) = 2↑↑↑...↑↑↑3 (with lgn(6) up-arrows)
Using the Bowers notation described earlier, lgn(1) is 2{12}3, and the entire Graham-Rothschild Number is just
2{2{2{2{2{2{2{12}3}3}3}3}3}3}3
This is the original number from Graham's proof.
As related by mathematician John Baez [62], Martin Gardner wanted to describe this in the Mathematical Games column of Scientific American, but Graham and Gardner agreed that the definition was a little too complex, and so they invented an even larger number...
The "Graham-Gardner Number"
This is the number commonly known as "Graham's number", but it is more attributable to Martin Gardner than to Graham. The number from the 1971 paper by Graham and Rothschild, described above, is an "upper bound". Upper bounds are "true" so long as the thing they're supposed to be "bounding" is provably smaller. That means you can use a larger number for an upper bound, and it's true too. If I tell you that 22×3=64 is an upper bound for my problem, then it's safe for you to tell someone else that 223=256 is an upper bound for the problem, because 256 > 64.
So Gardner and Graham came up with the definition for a larger upper bound, which was popularised by Martin Gardner in 1977. This came to be known as "Graham's number", but I call it the "Graham-Gardner number". Its value is gn(64), where gn() is defined as follows:
gn(n) = { hy(3,6,3) for n = 1 { { hy(3, gn(n-1)+2, 3) for n > 1
This illustration from the Graham's number Wikipedia article is a popular way to illustrate the definition concisely:
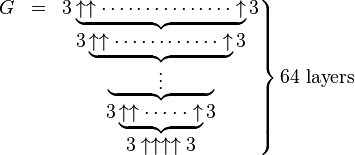
The "curly braces" indicate that the number of up-arrows in each "layer" is counted by the number immediately below, with 4 arrows in the bottom layer.
Todd Cesere and Tim Chow have both proven that the "Graham-Gardner number" is bigger than the Moser, and in fact even gn(2) is much bigger than the Moser. Tim's proof is outlined on a page by Susan Stepney, here.
Since gn(2) is 3{3{4}3}3 in Bowers notation, which is smaller than lgn(2) = 2{2{12}3}3, it follows that the "Graham-Rothschild number" is also bigger than Moser:
Moser << Graham-Rothschild << Graham-Gardner << Graham-Conway
This last variant, "Graham-Conway" is probably the least-known, but also the largest.
The "Graham-Conway Number"
Conway and Guy's book The Book of Numbers [48] includes a description of a "Graham's number" which is inexact, and which differs from the other "Graham's number" definitions above. The exact text from [48] is:
|
Graham's number is
4↑↑ . . . ↑↑4, where the number of arrows is 4↑↑ . . . ↑↑4, where the number of arrows is . . . et cetera . . . (where the number of lines like that is 64) It lies between 3→3→64→2 and 3→3→65→2. |
(The last bit with the right-arrows is using Conway's Chained Arrow Notation).
The problem with this description is that it doesn't tell you how many up-arrows you should start with, i.e. how many up-arrows are in the last of the "lines like that". We know there are 64 lines, and based on the other versions of "Graham's Number" described here it might be reasonable to imagine the number of arrows is 4, such that the last line is 4↑↑↑↑4=4{4}4, or we might assume 12 arrows such that the last line is 4↑↑↑↑↑↑↑↑↑↑↑↑4=4{12}4. The first possibility imitates the Graham-Gardner number simply using 4's instead of 3'3, while the other possibility imitates the Graham-Rothschild number. "Sbiis Saibian"40 has a thorough page on Graham's number [63] and calls this the "Graham-Conway number". He makes an educated guess that the number of up-arrows on the last 4↑..↑4 line should be the same as in the Graham-Gardner definition, i.e. 4 up-arrows: So we would say:
Graham-Conway Number = Gc(64)
where Gc(n) is defined for all positive integer n as follows:
Gc(1) = 4↑↑↑↑4
Gc(n+1) = 4↑↑...↑↑4 with Gc(n) up-arrows
With this clarification, the definition of the "Graham-Conway number" is just that of the "Graham-Gardner number" except that you change the 3's to 4's. This definition has a sort of elegance in that everything is 4's, even the number of lines can be expressed as 64=4×4×4 if you're really trying to use 4's everywhere.
If the starting number of arrows is 4 or more, then clearly the "Graham-Conway number" is larger than the others, and it's the largest "Graham's number" I've seen, notwithstanding xkcd:
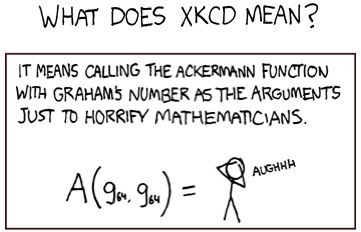
How to horrify mathematicians
This comic is using a 2-argument Ackermann function, and "g64" is meant to represent gn(64). There are several two-argument definitions in my listing (versions of Ackermann's function), and we could choose any of them. We may as well choose one that is easily turned into up-arrows, such as the one by Buck in 1963. This gives A(gn(64),gn(64)) = 2↑↑...↑↑gn(64), where the number of up-arrows is gn(64)-2. Thus it's "a little smaller" than gn(65). However, gn(A(64)) would be a lot bigger, because of the general principle that if you're going to apply one function to another, the way to get the largest result is to use the slower-growing function as input to the faster-growing one.
If xkcd wanted to horrify mathematicians a little more, and with fewer symbols than pictured above, they might be better off defining a "single-argument" Ackermann function a(x)=A(x,x), then subscripting one of the g's by this a() function:
ga(g64) = AAUGHHHH!!!
All of the Graham numbers are approximated by a 4-element Bowers Array, a notation that is discussed later, of the form [a,n,1,2]: Here they are expressed as a 5-element Bowers array, then using the "expanded" operator {{1}} which represents the recursively iterated hyper() function, and is the first of a hierarchy of recursive iterations of "expansion". We also approximate these with the fast-growing hierarchy:
Graham-Rothschild ≈ [3,7,1,2] = 3{{1}}7 ≈ fω+1(7)
Graham-Gardner ≈ [3,64,1,2] = 3{{1}}64 ≈ fω+1(64)
Graham-Conway ≈ [4,64,1,2] = 4{{1}}64 ≈ fω+1(64)
Fast Growing Hierarchy Functions of Infinite Order
In the fast growing hierarchy discussed earlier, each function fk() grows as fast as the "hyper" function with k+1 as the middle argument. And earlier, when first discussing function hierarchies we showed why it can be necessary to have sections in the function hierarchy that have an infinite number of functions, and therefore later functions that are "numbered" by larger-than-infinite indexes using Cantor ordinals. Now we have the opportunity to consider a function that grows faster than all finite-numbered functions, the first infinite-indexed function in a hierarchy that until now had just the finite-indexed hyper operators. As large as it is, gn(64)-2 up-arrows is still a finite number of arrows, and x↑↑...↑↑y with that many arrows is just one of the higher hyper operators.
But now, let's put the same number in all three arguments of the generalized hyper function, to make a function that grows faster than any fk() with a finite k:
g(x) = hy(x, x, x)
In the hierarchy popularly called "the" fast growing hierarchy (and less ambiguously called the hierarchy of Löb and Wainer), this g(x) is equivalent to fω(x), the first function with an infinite subscript.
hy(x, x, x) grows about as fast as fω(x)
The various Graham's numbers discussed in the previous sections all use the idea of iterating the 3-argument hyper function hy(a, n, b), in which the middle argument n is equal to hy(a, n, b) using a previous value of n. As we saw with the finite-indexed functions fk(), adding 1 to k means iterating the function, so fk+1(x) is just starting with fk(x) and substituting fk(x) for the x, iterating x times.
Therefore, the iteration process used in the Graham numbers is just the next index after fω():
The Graham-related functions lgn(x), gn(x), and Gc(x) all grow about as fast as fω+1(x)
So for example, gn(64) is "about" as big as fω+1(64), and the xkcd "how to horrify" number is fω+1(65). This is explained near the end of the "TREE vs Graham's Number" Numberphile video mentioned earlier.
Goodstein sequences (strong)
Let's return to Goodstein sequences again. This time we are using the "strong" definition of the iteration method, which employs the full "hereditary superscripts" expansion as described on the Wikipedia page and this page by Justin Miller. For example, the strong Goodstein sequence of 4 is OEIS sequence A56193 (you may wish to compare to the weak Goodstein sequence of 8, OEIS sequence A271989).
The hereditary base-b representations are analogous to ordinal infinities and subtracting one works like a "precessor function" on ordinal infinities — this means to subtract one from the finite component if any, and otherwise replace the lowest-rank ω with any finite number of your choosing. When the latter happens the number of ωs decreases by one and the number of ωs never increases. Therefore another ω will eventually be decreased to a finite value. Since each ω is always replaced by a finite number (no matter how big that might be), the total time to convert every individual ω to a finite values is the sum of a finite number of finite numbers, and this is also finite. Therefore the Goodstein sequence will eventually go down to zero.
The convergence of a series with no second-level exponents is easy to see:
v2 + 2
v2 + 1
v2
v2 - 1 = (a-1) × v + (a-1)
where a = value of v at this step
...
(a-1) × v
(a-2) × v + (b-1)
where b = value of v at this step
...
(a-2) × v
(a-3) × v + (c-1)
where c = value of v at this step
...
2 v
v + (d-1)
where d = value of v at this step
...
v
e - 1 where e = value of v at this step
When higher-level exponents are involved, the series will get longer each time a higher-level exponent has to be decremented. Each time the series will become enormously longer, but will still be of finite length. Therefore, the same principle applies.
Consider just one of the digits in that sequence, and call it "c". Suppose you are confident that all less-significant digits will keep getting smaller until they are all zero; then "c" will eventually get decreased to a lower number. Call that number "d" (which is c minus one). At this point the iteration continues for an even longer time with no change to "d" or any of the higher "digits", but eventually as before, the lowest digit "d" will have to get dinimished again.
Certainly we are confident that the lowest digit is always definitely going to reach zero; so this means the 2nd-lowest digit will diminish. It will then also reach zero, and the same argument applies to the next digit, and so on.
So in this way we see that each digit will eventually get replaced with a lower one. Each step takes massively longer than the previous step, but all steps are still of a finite length (not an infinite length) so eventually even the highest digits will get decreased.
Defining G(n) as the number of steps required to reach 0, With small arguments we can find values. From Googology and the Numberphile: video Way Bigger,,,Goodstein Sequence, estimates and bounds exist for slightly larger (but still small) arguments:
G(1) = 2
G(2) = 4
G(3) = 6
G(4) = 3×2402653211-3
10↑↑10↑↑10↑↑(10101020) < G(5) < 4↑↑↑8
2↑↑↑↑9 < G(6) < 6↑↑↑↑↑12
10↑↑↑↑↑↑↑9 < G(7) < 8↑↑↑↑↑↑↑16
A(A(G(4))) < G(8) < {3,4,1,2}
A(A(A(G(5)))) < G(9) < {4,5,1,2}
A(A(A(A(A(G(6)))))) < G(10) < {6,7,1,2}
A(A(A(A(A(A(A(G(7)))))) < G(11) < {8,9,1,2}
Graham's number < G(12) < {G(4),G(4+1),1,2}
...
in 1995 Bill Dubuque gave another outline of Goodstein sequences, and a description of the proof that they always reach zero.
Beyond the "strong" definition of Goodstein sequences, in which the bases are increased by one each time, there is remarkably an even faster-growing definition of Goodstein sequence in which the bases can increase by more than one. For example, you could increase the base by two at each step, or by three — you can even double the base at each step. Such versions of are called "extended" Goodstein sequences, and remarkably, the results of Goodstein's sequence still apply, per the same logic as in the previous paragraphs.
Friedman Block Subsequence Length: n(k)
In a 1998 paper[50], Harvey M. Friedman describes the problem of finding the longest sequence of letters (chosen from a set of N allowed letters) such that no subsequence of letters i through 2i occurs anywhere further on in the sequence. For 1 letter {A} the maximum length is 3: AAA. For 2 letters {A, B} the longest sequence is 11: ABBBAAAAAAA. For 3 letters {A, B, C} the longest sequence is very very long, but not infinite. It is in fact finite for any (finite) N, a result called "Friedman's block subsequence theorem".
He then goes on to show how to construct proofs of lower bounds for N-character sequences using certain special (N+1)-character sequences. With help from R. Dougherty, he found a lower bound for the N=3 case, A7198(158386) = ack-f(7198,158386) = ack(7198,2,158386) = hy(2,7199,158386) = 2(7199)158386, where x(7199)y represents the 7199th hyper operator.[54]
This value is less than the "Graham-Rothschild number" above, and all the other "Graham's number"s, but the N=4 case gives a result that is immensely bigger than all the versions of Graham's number. Friedman describes these relations at [57].
The block subsequence problem foreshadows two later fast-growing sequences also from Harvey Friedman: sequences of tree graphs leading to the TREE[] function; and sequences of sub-cubic graphs leading to the SSCG() function; both are discussed later.
Superclasses
Now let's take a break from the specific examples and functions for a moment to describe another type of "number class" that is evident in the way people relate to large numbers. We'll call these superclasses.
I first saw something like this in Eliezer Yudkowsky's description8 of the "Graham-Gardner number" described above. Yudkowsky was outlining the first few steps to that number, which are 3↑3, 3↑↑3, 3↑↑↑3, and 3↑↑↑↑3, as described by Martin Gardner in his Mathematical Games column, Scientific American, November 1977 (also in a book 16). Gardner spoke about whether the numbers could be printed or expressed "in any simple way". To this Yudkowsky added the ideas of "visualize" or "understand", which apply to varying extent to the numbers themselves and to the process for calculating them. I am adapting these ideas further to illustrate "superclasses" (as with classes I am defining a special lsrge numbers-related meaning for this word).
Superclass 1 includes numbers that could be described as being small enough to "visualise", which means being able to form a mental image of that number of objects. If the numbee is 7 or 12, "visualizing" means closing one's eyes and seeing seven apples or twelve trees. Yudkowsky used the number 27 as an example, because (as in Gardner) 27=3↑3 is the first step in imagining the construction of the Graham-Gardner number. Superclass 1 extends a but further than class 0 (subitizing), but not as far as class 1 because if you close your eyes and try to picture 100,000 things, you'll probably have the same perception as if you tried 1,000,000.
Superclass 2 encompasses numbers that are too large to visualize but can be "understood". An example of this might be 5×1014, the surface area of the Earth in square metres. Even 5 million is too big for anyone to visualise, but most people could understand that it is the surface area of the Earth in square metres. Another example of similar magnitude is the number of cells in a human body. (Yudkowsky and Gardner used 3↑↑3 = 7625597484987 as the example here; Gardner described it as being "still such a small number that we can actually print it".
Superclass 3 is for numbers that are beyond understanding, as their description is too abstract or remote from human knowledge and experience. An example on the very low end of this range is 2↑↑1000, the very largest entry in my "numbers" list, which is the value of 2↑2↑2↑...↑2, an "exponential tower" of 2's that is 1000 units high. This number was used in a proof by Harvey Friedman. It is far larger than anything in the real world, or even combinations of things (such as the number of ways to shuffle every particle in the known universe) — all such numbers only require, at most, 4 or 5 levels of a power-tower to express.
So, 2↑↑1000 represents a quantity far beyond comprehension. But Yudkowsky (using 3↑↑↑3 as the example) states that "the procedure for computing it can be visualised": we start with x=2, then calculate 2x (by repeated multiplications), then have that be the new x and do a new calculation for 2x, and so on until you've done it 999 times. Not only can it be visualized, it could be done in a reasonable amount of time on a computer using the level-index representation format or something similar (be advised: some round-off approximation may occur :-).
For Superclass 4, we have 3↑↑↑↑3, the first step in the definition of the "Graham-Gardner number" described above. Working this out through repeated exponentiation would take an unimaginable number of exponentiation steps. It is 3④(3④(3④(...④(3④3))...)), a chain of 7 trillion 3's and hyper4 operators. Most all of these requires performing the exponent operation an incomprehensible number of times. So length of time it would take to do such a task is beyond human ability to visualise, but it can be "understood".
If you think of it as tetration (hyper4) steps, there are "only" 7 trillion tetrations required. There are number representation formats (such as OmegaNum.js) that can handle this sort of thing easily and print out the nice concise answer "10^^^(10^)^7625597484984 3638334640023.7783". Any human perception of this answer, in relation to any actual qualtity it represents, is necessarily abstract. As Gardner stated,
3↑↑↑↑3 is unimaginably larger than 3↑↑↑3, but it is still small as finite numbers go, since most finite numbers are very much larger.
Now for Superclass 5. We have just seen four numbers in a sequence: 3↑3, 3↑↑3, 3↑↑↑3, and 3↑↑↑↑3. Consider the formula for the "Graham-Gardner number". We begin with x = 3↑↑↑↑3, the number whose calculation procedure cannot even be visualised — then increase the number of up-arrows from 4 to x. Then increase the number of up-arrows to this new, larger value of x again. Then — repeat 61 more times! Here's what Yudkowsky had to say:
Graham's number is far beyond my ability to grasp. I can describe it, but I cannot properly appreciate it. (Perhaps Graham can appreciate it, having written a mathematical proof that uses it.) This number is far larger than most people's conception of infinity. I know that it was larger than mine. ...
This example illustrates the numbers (including those on my numbers page and on this page up to this point) can be seen as going from one level of abstraction to another. Here are the definitions of the superclasses:
Superclass 1: The number can be visualised. (Example: 27)
Superclass 2: The number cannot be visualised but it can be understood. (Example: 3↑↑3 ≈ 7 trillion)
Superclass 3: The number cannot be understood, but the procedure for computing it can be visualised. (Example: 3↑↑↑3)
Superclass 4: The procedure cannot be visualised, but the procedure can be understood. (3↑↑↑↑3)
Superclass 5: The procedure for generating the number is so abstract that it cannot be understood (by whoever's talking, by the author, by yourself, by some given group or people, etc.).
To complete the analogy to the normal classes, I will also add:
Superclass 0: The number can be "experienced" even by certain animals. (Example: 2)
Like the classes, the superclasses have important qualities that distinguish them, and this insight is what makes "superclass" a useful distinction. Each requires an additional type of mental effort to ensure that the number is understood well anough to answer questions such as which number is larger, or which algorithm grows faster.
Notice that the first three (superclass 0, 1 and 2) roughly parallel class 0, class 1 and class 2 above. The division points between them will be similar for most readers, but the upper range of superclass 2 will probably vary a lot from one reader to another. I think I "understand" numbers about as big as the size of the visible universe, although I find it harder on some days than on others. There are probably people who have an understanding of such things as the size of the universe after cosmic inflation, or the size that would be needed for a spontaneous origin of life.
The first three superclasses can all be calculated fairly easily, using familiar techniques or modest towers of exponents. Even with towers of exponents, relative size questions can easily be answered by looking at the number of levels in the tower and the value of the number at the top. Practical tools like hypercalc exist to actually work with these numbers.
Superclass 3 begins wherever one's ability to "understand" ends. However, the procedure for computing it can still be visualised. Somewhere within superclass 3, hypercalc stops working but more sophisticated formats like that of OmegaNum.js are still able to work. We well beyond the ability to work with actual numbers and have to start using symbols and words, but it is still possible to make fairly simple proofs to show how one function converts to another. Examples include the "power tower paradox", and proving that the higer-valued hyper4 operator a④b grows about as quickly as the lower-valued hyper5 operator a⑤b.
With superclass 4, such proofs become more difficult. This is why it is a bit tougher to compare the "Graham-Rothschild number" to the Moser. It can be worked out by most who have time and patience, and the explanation can be followed and understood fairly easy, but it probably isn't too easy to remember.
With Graham's number (the original "Graham-Rothschild number" or its more well-known variant the "Graham-Gardner number"), and other numbers of similar size and larger which we are about to get into, most readers will have stepped firmly into superclass 5. The last paragraph in the Yudkowsky quote captures what superclass 5 is about: perception and understanding are so difficult that it is hard even to compare the number to infinity. I cannot say where your superclass 5 begins, but once you reach it, it is better to stop trying to grasp the quantities in any direct way and instead use rigorous deduction, or trust others who have done so.
Since I first published this discussion, the ability for people to understand abstractions of large number definitions has been greatly improved by easily accessible online explanations. There is even an online game called Ordinal Markup in which a memorable goal, achieved fairly early in the game, is to get your score up to Graham's number. Such games and the "googology" community at large have broadened popular understanding of such things as up-arrow notation.
So, perhaps a better example of superclass 5 would be Jonathan Bowers' "gongulus" which is {10, 10 [100] 2} in Chris Bird's multi-dimensional array notation. It is the value of a Bowers dimensional array with 100 dimensions, length 10 on each side, containing all 10's (a googol 10's in total). If that's not incomprehensible enpough for you, then perhaps your superclass 5 starts higher. I suspect it would include Rayo's number, which is defined so abstractly that no actual fast-growing function definitions need to be stated.
I have found my own boundary between 4 and 5 varies widely from one day to another. Clearly there are those (such as the people who worked on the numbers we are about to discuss) for whom "superclass 4" extends far higher than mine. I suggest it might be useful to define:
Superclass 6: The number is so big that no-one can understand its definition well enough to know anything useful about it.
In other words, superclass 6 is finite, but so large that no person, nor humanity as a whole, stands a chance of discovering anything tangible about it. This probably happens with values of the Busy Beaver function with an argument greater than a few hundred.
Conway's Chained Arrow Notation
This notation is based on Knuth's up-arrow notation. In this notation, three or more numbers are joined by right-arrows (→). The arrow is not an ordinary dyadic operator. You can have three or more numbers joined by arrows, in which case the arrows don't act separately, the whole chain has to be considered as a unit. It might be thought of as a function with a variable number of arguments, or perhaps a function whose single argument is an ordered list or vector.
I wrote a thorough description of Conway chains, including how a chain can be interpreted, and in some cases converted to earlier notations, based on Susan Stepney's descrpition from here. The important points are:
a→b = ab
a→b→c = hy(a,c+2,b) = a↑↑...↑b (with c up-arrows)
a→b→n→2 is an iteration like Graham's number, starting with a↑b and applying n-1 steps
a→b→n→3 is staggeringly larger
with a→b→c→d→e and longer chains, things start to get really interesting...
From this and the longer descriptions in the links, it is easy to see
3→3→64→2 is like the Graham-Gardner number except starting with 3↑3 instead of 3↑↑↑↑3
3→3→64→3 is 3→3→(3→3→(3→3→(...(3→3)...→3)→3)→3)→2, which is like the Graham-Gardner number except starting with something a lot bigger than 3↑↑↑↑3
and so the Graham-Gardner number itself lies between these two.
Partial Ordering for Chained Arrows
One may speculate on the general problem of determining which is the larger of two chains a→b→c→...m→n and p→q→r→...→y→z. We can begin to answer that question for some of the shorter chains (most of which is simply a restatement and re-ordering of the examples in my partial ordering for Knuth up-arrows):
First, as noted above we can remove any 1's and anything coming after a 1. Also, if the chain starts with 2→2 the whole thing can be replaced with 4.
For two-item chains it's just a→b=ab, so the following are clear:
2→3 is smaller than 3→2
2→4 is the same as 4→2
for any other a and b, if b is greater than a then a→b is
greater than b→a.
Now let's look at three-item chains:
For any a, the chain a→2→2 = a↑↑2 = aa. So for these, the one with a larger a is the larger chain.
If the first two items are the same, as in comparing a→b→c to a→b→d, both are like a↑↑↑...↑↑↑b but one has more arrows. So if a and b are both greater than 2, then the one with the larger third item (c or d) is larger.
Similarly if the first and last items are the same, as in comparing a→b→d to a→c→d, we are comparing two things with the same number of arrows (a↑↑↑...↑↑↑c versus a↑↑↑...↑↑↑d) and clearly the one with the larger number in the middle (c or d) is larger.
A similar argument shows that if we are comparing a→c→d to b→c→d, where only the first number differs, the one with the larger first number is larger. This is a generalization of the a→2→2 case above.
2→3→2 = 2↑↑3 = 2↑2↑2 = 2↑4 = 16, but 2→2→3 = 2↑↑↑2 = 2↑↑2 = 2↑2 = 4. Since 2→2→anything is 4, it's clear that if we have two 2's, the arrangement with the larger-than-2 number in the middle is larger. Also, 3→2→2 = 3↑↑2 = 3↑3 = 27, so this is the largest of the three combinations of two 2's and a 3.
There are three ways to combine a 2 and two 3's:
3→3→2 = 3↑↑3 = 3↑27;
3→2→3 = 3↑↑↑2 = 3↑↑3 = 3↑27;
2→3→3 = 2↑↑↑3 = 2↑↑2↑↑2 = 2↑↑4
= 2↑2↑2↑2 = 2↑2↑4 = 2↑16 = 65536
Now let's look at the combinations of 2, 3 and 4. There are 6 of these, and I'll show them here with the smallest first:
4→3→2 = 4↑↑3 = 4↑4↑4 = 4↑256.
4→2→3 = 4↑↑↑2 = 4↑↑4 = 4↑4↑4, the same as 4→3→2
3→4→2 = 3↑↑4 = 3↑3↑3↑3, a power-tower of height 4
(or 3↑3↑27, a tower of height 3)
2→4→3 = 2↑↑↑4 = 2↑↑(2↑↑(2↑↑2)) = 2↑↑(2↑↑4)
= 2↑↑16, a tower of height 16.
2→3→4 = 2↑↑↑↑3 = 2↑↑↑(2↑↑↑2) = 2↑↑↑4,
the same as 2→4→3 (the same tower of height 16).
3→2→4 = 3↑↑↑↑2 = 3↑↑↑3 = 3↑↑(3↑↑3)
= 3↑↑(3↑3↑3) = 3↑↑(3↑27), a tower of height 327.
The thing to notice is that the winners have the 4 at the end, and among them the one with the 3 first is a lot larger. Let's look at those two again with bigger numbers all around:
4→3→5 = 4↑↑↑↑↑3 = 4↑↑↑↑(4↑↑↑↑4)
= 4↑↑↑↑(4↑↑↑4↑↑↑4↑↑↑4)
3→4→5 = 3↑↑↑↑↑4 = 3↑↑↑↑(3↑↑↑↑(3↑↑↑↑3))
= 3↑↑↑↑(3↑↑↑↑(3↑↑↑3↑↑↑3))
Here it appears that 3→4→5 is going to end up being larger than 4→3→5. This is a reflection of the general rule for partial ordering of the hyper operator described earlier.
Jonathan Bowers' Extended Operators
Jonathan Bowers has defined a whole series of notations that surpass everything mentioned so far. We can start by defining his extended operators, which are kind of analogous to the hyper operators. In fact, he starts with the hyper operators, which can be thought of as the original, "unextended" set of operators. Instead of putting the operator number inside a raised circle, he uses a pair of "angle-brackets":
a <n> b = aⓝb = hy(a,n,b)
So, <1> is addition, a <1> b = a+b; <2> is multiplication and so on.
Using this notation makes it easier to make the operator itself a variable or expression, and unlike using the hy() function it retains the look of applying an operator (because the operator part is in the middle where it "belongs". For example:
a <1+2> b = a <3> b = ab
gn(1) = 3 <6> 3
gn(2) = 3 <3 <6> 3> 3
Mega ≈ 256 <4> 2
Moser ≈ Mega <Mega+1> 2 ≈ (256 <4> 2) <256 <4> 2> 2
Here is his first extended operator:
a <<1>> 2 = a <a> a
a <<1>> 3 = a <a <a> a> a
a <<1>> 4 = a <a <a <a> a> a> a
and so on
a <<1>> b is "a expanded to b".
If you wish, you might prefer to represent this operator in a way similar to the higher hyper operators but with a 1 inside two circles (which I'll enlarge here for clarity):
a⓵b
Since the two circles are hard to see in normal font sizes, I'll instead use the hyper1 operator symbol ① inside a set of parentheses: a(①)b.
Using this notation, the "Graham-Gardner number" is shown to be between 3(①)65 and 3(①)66 (the gn(x) function is as defined here):
3(①)2 = 3 <3> 3
gn(1) = 3 <6> 3
3(①)3 = 3 <3 <3> 3> 3 = 3 <27> 3
gn(2) = 3 <3 <6> 3> 3
and so on
3(①)65
gn(64) = "Graham-Gardner number"
3(①)66
Going back to Bowers' notation, here is the definition of the next extended operator. It is a right-associative recursive iteration of the first:
a <<2>> 2 = a <<1>> a
a <<2>> 3 = a <<1>> (a <<1>> a)
a <<2>> 4 = a <<1>> (a <<1>> (a <<1>> a))
and so on
a <<2>> b = a <<1>> (a <<2>> (b-1))
a <<2>> b is called "a multiexpanded to b".
Note the similarity of the definition a <<2>> b = a <<1>> (a <<2>> (b-1)) to the corresponding definition for a hyper operator, e.g. a②b = a①(a②(b-1)).
The subsequent extended operators are defined in a similar way, each in terms of the previous.
a <<3>> b is called "a powerexpanded to b".
a <<4>> b is called "a expandotetrated to b".
Then Bowers defines a third series of extended operators, in a similar way:
a <<<1>>> 2 = a <<a>> a
a <<<1>>> 3 = a <<a <<a>> a>> a
a <<<1>>> 4 = a <<a <<a <<a>> a>> a>> a
and so on
a <<<1>>> b is "a exploded to b".
then the next operator:
a <<<2>>> 2 = a <<<1>>> a
a <<<2>>> 3 = a <<<1>>> (a <<<1>>> a)
a <<<2>>> 4 = a <<<1>>> (a <<<1>>> (a <<<1>>> a))
and so on
a <<<2>>> b is called "a multiexploded to b".
and so on:
a <<<3>>> b is called "a powerexploded to b".
a <<<4>>> b is called "a explodotetrated to b".
You can see that this generalises easily to a function of four numbers, a, b, the number inside the angle-brackets and a number telling how many angle-brackets there are. This can be written as a function, f(a,b,c,d) or something like that — but Bowers wanted to go further.
First page . . . Back to page 5 . . . Forward to page 7 . . . Last page (page 11)
Japanese readers should see: 巨大数論 (from @kyodaisuu on Twitter)
If you like this you might also enjoy my numbers page.
 s.30
s.30