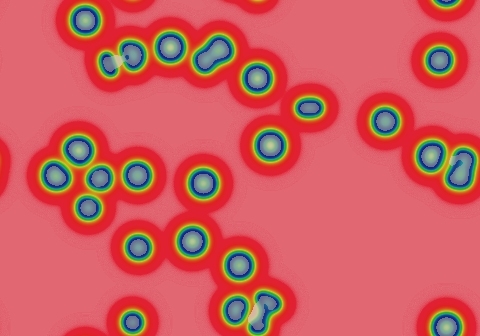
Gray-Scott Model at F 0.0740, k 0.0610

These images and movie demonstrate the behavior of the Gray-Scott reaction-diffusion system with σ=D_u/D_v=2 and parameters F=0.0740, k=0.0610.

Loops grow into clovers and become more convoluted; worm tips bud off from tight bends. Worm tips continue to grow, pushing other objects aside, and can fuse with each other to link the otherwise autonomous structures together. Smaller loops tend to get squeezed out; the result is almost all mostly straight parallel lines. This process takes well over 500,000 tu.

If initialized with a negative type pattern, these parameters produce phenomena like those to the south, but once the space is filled with loops, the evolution proceeds in a way very similar to that seen here. (glossary of terms)

	increase F
decrease k	15 frames/sec.; each fr. is 252 iter. steps = 126 tu; 1800 fr. total (226,800 tu)	increase k

	decrease F

(Click on any image to magnify)

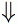In these images:

Color indicates level of u, ranging from purple (lowest u values) through blue, aqua, green, yellow and pink/red (highest u values)
Areas where u is increasing are lightened to a light pastel tone; where u is decreasing the color is vivid.
In areas where u is changing by less than ±3×10^-6 per tu, an intermediate pastel color is seen. This includes areas that are in steady state or equilibrium.

Wavefronts and other moving objects have decreasing u values (brighter color) on the leading edge of the blue part of the moving object, and increasing u (light pastel color) on the trailing edge. This is true even for very slow-moving objects — thus, you can tell from the coloring what direction things are moving in.

''tu'' is the dimensionless unit of time, and ''lu'' the dimensionless unit of length, implicit in the equations that define the reaction-diffusion model. The grids for these simulations use Δx=1/143 lu and Δt=1/2 tu; the system is 3.2 lu wide. The simulation meets itself at the edges (periodic boundary condition); all images tile seamlessly if used as wallpaper.

Go back to Gray-Scott pattern index

This page was written in the "embarrassingly readable" markup language RHTF, and was last updated on 2015 Nov 07.

s.27