Mu-Unit
Robert P. Munafo, 2023 Mar 13.
I use the term mu-unit to refer to a subset of the Mandelbrot set that is tuned by one of the mu-atoms. A mu-unit is a set S with the following properties:
1. S is a subset of R2.
2. S is topologically equivalent to (i.e., maps after distortion
onto) R2.
3. The boundary of S is a subset of the boundary of R2.
The concept of mu-unit is fundamental to an understanding of the visual structure of the Mandelbrot Set. As stated in the definition, a mu-unit "maps aftrer distortion onto" the entire Mandelbrot Set. This "distortion" is nonlinear and appears smooth, although it is probably actually nondifferentiable.
Every mu-atom has a mu-unit. Because there are two types of mu-atoms (seeds and descendants, q.v.) there are two types of mu-units. The two types are equivalent but have a different visual appearance. We can call them "seed mu-units" and "descendant mu-units".
A seed mu-unit is an island mu-molecule, together with its collection of filaments and smaller mu-molecules. Each of the filaments in the mu-unit correspond to a filament in the whole Mandelbrot Set; any filament that does not correspond to something in the whole Mandelbrot Set is not part of the mu-unit. With some island mu-molecules it is easy to see which filaments belong to the mu-unit because the mu-unit filaments are visibly denser.
A descendant mu-unit is a descendant mu-atom along with such filaments as correspond in a one-to-one way with the whole Mandelbrot Set. It is not visually easy to distinguish which filaments belong to the mu-unit, so I will try to illustrate the difference :
 R2.1/3 and surrounding filaments | A .__a- '._,, _r` `'~v_"` .\ __Y` _ ^ ~_/,,~ B ._'T/.[, _ ~-- ."` "''-,-` -/` '\ _, _ , __-`~- ^:mdL- 'e//br", '^` ba, _/v/-F` '" ^e^`` _'dF`. ---\%m(L , '"- _.:`@-., _., . , `\YccC,,d"m/T)[-, m**` ':*., _^TF:"` -*(_(mF-v- '^"m" , _ -""b7 b(m_ _` ._.$-..(_\m_C^ '*-"`-.,'"), .r$'` ._, "(.:d^` ''`:)"* ' :be,,-__ -a%"e@*^``^` -*v-/b.:$-- `"d"^ ^ .^"Y%ceL)e$'` '^^:C- a_ ^*c-_m._, -"*"%; ')` ^`@v7\\T[bb" '*m~` -`"[:, ^^ `@`Yr/ \aee -\"Y rm"~`~ .,m"7^,vLC` -:F` /_\.- ~`* 'F@%_. C *([,_Y-e' ._L^*C .\_/[""'`` .@*\F^c "Y`-cv, '' :%;C .r"""`" '"")/,, .ad"Y` ._.._ ^`@)c, _,mF"` :_ _,$Fd@, _:em a,,__ _''~-.._ ._.,-`^ _ _,.e,, .)a_ -v@md_ ^'^^^^` `^`^'^`''^'^^`^`^'^``^ ^^^^^^`^'^``^^''`^`'^^^` ^^^^^'` Figure 1. The mu-unit R2.1/3, along with many filaments that are not part of it. Points A and B are the two main branch tips, and point C is the mu-atom's center. |
 Mu-unit R2.1/3 | D , '[ .' ] ,:,, -\.-* '-c_r- ./` .\, ^, ." ._ __.__;- E -`..,_, _, '(~--`` ''--") A ^.,_..,.m-` `-v .--__r '^^]; `~ '-^ C. ^^ B '"--r -,"~" _e ',_ . ,"- ]`, . '):[;, [^]:< '`^` '^^ -,:~ _`c_ ^^^` :"'^` "~", .:-"^ ``,_, __:'` ^"-_,, ._a-"` ^^^` F '^^'^ Figure 2: The mu-unit R2.1/3. (This is an imprecise rendering: in particular, the "antenna" at the top should be taller.) See text for explanation of labeled points A through F. |
In the ASCII version of figure 2 the letters A, B, and C can be seen at about the 2 o'clock position, and indicate the parts of the mu-unit which correspond to the points A, B, and C in figure 1. Point D (very top) corresponds to R2t, the leftmost tip of the Mandelbrot Set; point E (middle) corresponds to R2.C(1/2), the "seahorse valley" area at -0.75+0, point F (bottom) corresponds to R2.C(0), the cusp at 0.25+0i.
At first glance, the mu-unit is just a rotated, distorted copy of the Mandelbrot Set (See the entry on R2 for a picture of the whole Mandelbrot Set):
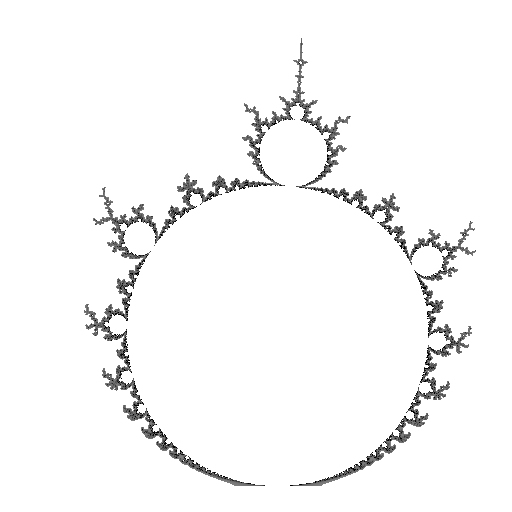 R2.1/3 |
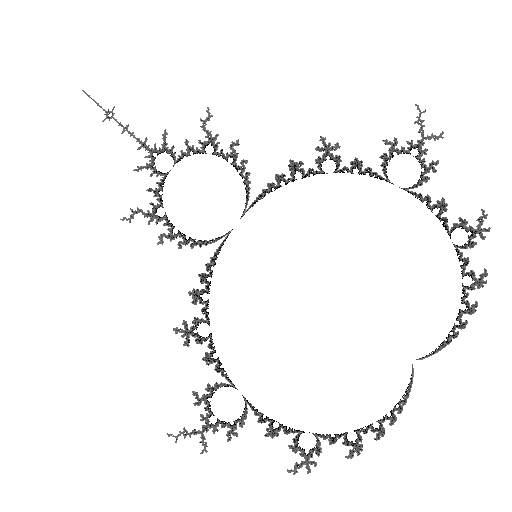
 ... |
 ... |
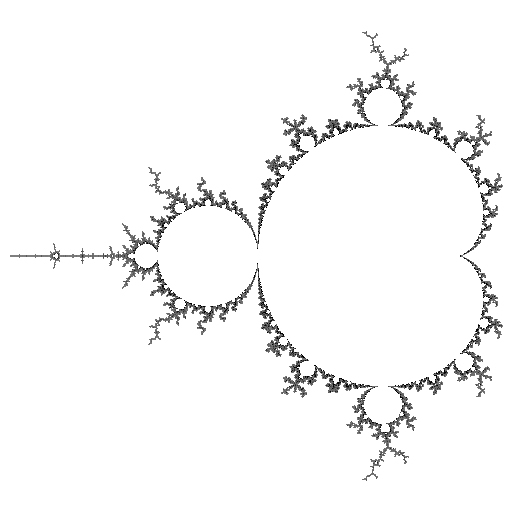 R2 |
Upon closer inspection one always finds areas of the mu-unit where the distortion is arbitrarily great. For example, if you use the computer to view the area near points A and B in figure 2, you will see that the branches are "stretched out" a fair amount in comparison with the corresponding features in Figure 1, and the curvature of their geometric spirals is quite different. This localized distortion becomes more pronounced as you approach a cusp (like point F) or a tip (like point D).
I refer to the largest, lowest-period atom in a mu-unit as the mu-unit's owner.
revisions: 19960207 oldest on record; 20100917 add color images, expand figure 2 caption; 20120818 slightly clarify the definition; 20230216 add "intermediate steps" images; 20230313 improve caption for distortion steps
From the Mandelbrot Set Glossary and Encyclopedia, by Robert Munafo, (c) 1987-2024.
Mu-ency main page — index — recent changes — DEMZ
This page was written in the "embarrassingly readable" markup language RHTF, and was last updated on 2023 Mar 14.
 s.27
s.27