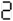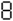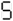Notable Properties of Specific Numbers
First page . . . Back to page 6 . . . Forward to page 8 . . . Last page (page 25)
(the quintessential Kaprekar number)
|
Kaprekar numbers
452 = 2025, and 20+25 = 45. Numbers like this are called Kaprekar numbers. There are a few ways to define the sequence, depending on whether you allow dividing the square into two "pieces" of unequal size (for example, see 4879) and whether a trivial case like a power of 10 should count. I interpret the Kaprekar numbers the way they were originally described by Wells: If the original number N has D digits, then after squaring you should split it into a "right half" of D digits, equal to N2 mod 10D, and a "left half" of D or D-1 digits, equal to floor(N2/10D). Using those rules, the sequence of Kaprekar numbers runs: 1, 9, 45, 55, 99, 297, 703, 999, 2223, 2728, 4950, 5050, 7272, 7777, 9999, 17344, 22222, 77778, 82656, 95121, 99999, 142857, ... (Sloane's A53816, more terms here)
The Kaprekar number concept can be extended to higher powers. 453= 091125, and 09+11+25=45. The numbers with this property are: 1, 8, (10), 45, 297, 2322, 2728, 4445, 4544, 4949, 5049, 5455, 5554, 7172, 27100, 44443, 55556, 60434, 77778, 143857, ... (more terms here). 10 is shown in parentheses because some folks consider it to be too trivial to count, however it does meet the requirements of the formula: 103=1000, break 1000 into groups of 2 digits starting from the right, 10+00=10.
45 is also a Kaprekar number for 4th powers: 454=04100625; 04+10+06+25=45. This sequence runs: 1, 7, 45, 55, 67, (100), 433, 4950, 5050, 38212, 65068, ... (more terms here)
45 is the only number (up to at least 400000) that is in all three of these Kaprekar sequences.
45 is the magic constant (row or column sum) of Lee Sallows' "alphamagic square", which is the following non-regular magic square:
|
with the property that if you put the numbers in words:
|
and then count the letters, you get another magic square (this time with magic constant 21):
|
(from John D. Cook)
45 is also the magic constant of this invertible non-normal magic square:
|
when turned upside-down you get this:
|
with magic constant 153. Alternatively instead of turning the whole square upside-down you could just exchange the 10's and 1's digits of each number to get:
|
also with magic constant 153.
Distinct Semiprimes
46 is the product of two distinct primes. This sequence, a subset of the semiprimes, begins: 6, 10, 14, 15, 21, 22, 26, 33, 34, 35, 38, 39, 46, 51, 55, 57, 58, 62, 65, 69, 74, 77, ... (Sloane's A6881). A similar sequence requiring the two primes to be consecutive is discussed in the entry for 77.
The first of three consecutive primes that are spaced an equal distance apart: 47, 53 and 59 are spaced 6 apart and have no other primes in between. The first such set of 3 primes is (3, 5, 7); the next three are (151, 157, 163) and after that it becomes a bit more frequent. See also 251, 9843019, 121174811, 19252884016114523644357039386451 and 2.0014732742×1051089.
47 is a member of a sequence with a simple definition and a few interesting properties. The sequence begins with 3 and each successive term An+1 is An2-2. This is just like the definition of the Lucas-Lehmer sequence but starting with 3 instead of 4. The sequence starts: 3, 7, 47, 2207, 4870847, 23725150497407, 562882766124611619513723647, ... (Sloane's A1566). Each term An is equal to the ratio F2n+2 / F2n+1 where Fn are the Fibonacci numbers (for example, F16/F8 = 987/21 = 47).
Also, every term is relatively prime to every other term, something I call mutually co-prime. (The Sylvester sequence is another example). This can be demonstrated by considering what happens when you show the terms of the sequence in base p, where p is any prime number. Before looking at a prime base, consider base 10 — the first term is 3, and after that every term ends in 7. It is easy to see why — whenever you start with a number ending in 7 and calculate n2, you'll get a number ending in 9 — then after subtracting 2, it will end in 7 again. Stated more tersely, 72-2 = 7 mod 10. Here are the first 5 terms of the sequence in four other bases:
|
Notice the final digits highlighted in bold. In base 7, the second term ends in 0, because the second term is divisible by 7. The next term ends in 5, which is 2 less than the base — because of the "minus 2" in the formula An2-2. The term after that ends in 2, because 52-2 is 23, which in base 7 is 327, ending in 2. It is true in any base that (b-2)2-2 = 2. And after that, all following terms will also end in the digit 2, because 22-2 = 2. Similarly, if there is any term that is divisible by the prime p, that term will end in 0 in base p, the following term will end in p-2 and all terms after that will end in 2. Therefore, only one term is divisible by p for any prime p, and it follows that every term is relatively prime to every other term. The table illustrates the same thing happening in base 3 and base 47. In general, considering any two terms Ai and Aj, where i<j, looking at the final digit in base Ai shows that Ai is relatively prime to Aj.
The base 11 case demonstrates another interesting fact: that there are some prime numbers that divide into none of the terms of the sequence. In base 11, the final digit alternates between 3 and 7 forever. Thus, no terms are divisible by 11.
The "47 percent" are a group of voters in the United States who notionally have a victim mentality and expect publicly-funded institutions to provide some sort of social equity.
(a composite that is not semiprime)
Notable for having a lot of factors: 48 is 24×3 and is divisible by 2, 3, 4, 6, 8, 12, 16, and 24.
One of a sequence (A33942 in the OEIS) of numbers that have at least three prime factors (as with 48, the three primes do not need to be distinct, so for example 8=23 counts as the product of 3 primes). The sequence starts: 8, 12, 16, 18, 20, 24, 27, 28, 30, 32, 36, 40, 42, 44, 45, 48, 50, 52, 54, 56, 60, 63, 64, 66, 68, ... Some of the numbers in this sequence are divisible by three different primes. The composite numbers not in this sequence are called semiprimes.
48 and many of the smaller numbers in the A033942 sequence are also 3-smooth numbers.
49 = 7×7, the square of a traditionally "lucky" number. 49 is also "lucky" in another sense.
Stanislaw Ulam devised a sequence of numbers called lucky numbers. The sequence is generated by a sieve similar to the Sieve of Eratosthenes that (can be) used to generate the sequence of primes. The lucky numbers are: 1, 3, 7, 9, 13, 15, 21, 25, 31, 33, 37, 43, 49, 51, 63, 67, 69, 73, 75, 79, 87, 93, 99, 105, 111, 115, 127, 129, 133, 135, 141, 151, 159, 163, ... (Sloane's A0959). These numbers share a few interesting properties with the primes, most of them similarities in statistical distribution.
This is 232 milliseconds converted to days (that is, 232/(1000*86400). Early in 1999, Microsoft warned users that "after exactly 49.7 days of continuous operation, your Windows 95-based computer may stop responding". The bug was caused by a Y2K-like problem on a shorter time scale. There is a time counter (accessible through the functions GetTickCount, "GetTickTime" and/or "GetSystemTime") that counts milliseconds since the time the computer was started; when this wrapped around from 232-1 back to 0, some DLL or driver got confused and stopped functioning, making the system "hang".
See also 2147483647 and 11644473600.
50 = 12+72 = 52+52, the smallest number that is the sum of squares in two different ways (if the squares must be distinct, it would be 65). The numbers with this property are: 50, 65, 85, 125, 130, 145, 170, 185, 200, 205, 221, 250, 260, 265, 290, 305, 325, 338, 340, 365, 370, 377, ... (Sloane's A7692). See also 1729 and 635318657.
50 is also the sum of three consecutive squares: 32+42+52=50 (see 216).
Also a magic number in nuclear physics.
(Motzkin numbers)
51 is a Motzkin number. These numbers count combinations of things, in a way similar to the Bell and Catalan numbers. In this case, they count certain orderings of parentheses, or connected paths on a unit grid, or noninteresting chords on a circle. The sequence starts: 1, 1, 2, 4, 9, 21, 51, 127, 323, 835, 2188, 5798, 15511, 41835, 113634, 310572, 853467, 2356779, 6536382, ... (OEIS sequence A1006). The following illustrates the first few Motzkin numbers (notice the similarities and differences to the Catalan numbers):
(For a time this was listed as an "uninteresting" number, but now I discuss that here; see also 12407.)
Left side illustrates: Right side illustrates: Number of paths of N steps Number of distinct ways where each step goes east, parentheses can be substituted northeast or southeast, and for X's in a string of N never goes further south characters, with the than the starting point. parentheses balanced. A[1] = 1 _ x A[2] = 2 __ /\ xx () _ A[3] = 4 ___ _/\ /\_ / \ xxx x() ()x (x) _ ____ __/\ _/\_ _/ \ xxxx xx() x()x x(x) _ __ A[4] = 9 /\__ /\/\ / \_ / \ ()xx ()() (x)x (xx) /\ / \ (()) xxxxx xxx() xx()x xx(x) x()xx x()() x(x)x x(xx) A[5] = 21 x(()) ()xxx ()x() ()()x ()(x) (x)xx (x)() (xx)x (xxx) (x()) (())x (()x) ((x)) A[6] = 51 xxxxxx xxxx() xxx()x xxx(x) xx()xx xx()() xx(x)x xx(xx) xx(()) x()xxx x()x() x()()x x()(x) x(x)xx x(x)() x(xx)x x(xxx) x(x()) x(())x x(()x) x((x)) ()xxxx ()xx() ()x()x ()x(x) ()()xx ()()() ()(x)x ()(xx) ()(()) (x)xxx (x)x() (x)()x (x)(x) (xx)xx (xx)() (xxx)x (xxxx) (xx()) (x())x (x()x) (x(x)) (())xx (())() (()x)x (()xx) (()()) ((x))x ((x)x) ((xx)) ((()))51 is called a "pentagonal" number by both definitions of the term. In the first, a triangle is put on top of a square. The other uses a symmetrical pentagon arrangement:
4 6 4 4 5 6 4 3 4 4 5 6 4 3 3 4 3 4 5 6 4 3 2 3 4 2 3 4 5 6 3 2 2 3 1 2 3 4 5 6 4 2 1 2 4 2 2 3 4 5 6 3 1 1 3 3 3 3 4 5 6 4 2 0 2 4 4 4 4 4 5 6 3 1 1 3 5 5 5 5 5 6 4 2 2 2 4 6 6 6 6 6 6 3 3 3 3 4 4 4 4 4 0+1+4+7+10+13+16+... 1 + 5 + 10 + 15 + 20 + ... (3n^2-n)/2 (5n^2+5n+2)/2 for n in {0..6] for n in [0..4]See also 3151.
The Aperiodical created a service at isthisprime.com, that tells you if a number is prime (for example: 2186969441? Yes.) Then, just for fun, they created the online "Is this prime" game, in which you, the human, try to name numbers as prime or composite, with a time limit. After collecting statistics for a couple months, they found that 51 is the number people most commonly get wrong (it narrowly beat out 57). 51 is 3×17.
(Bell numbers)
52 is one of the Bell numbers: 1, 1, 2, 5, 15, 52, 203, 877, 4140, 21147, 115975, 678570, 4213597, ... (Sloane's A0110). These numbers count the number of ways of putting n distinguishable balls into one or more indistinguishable urns. For example:
1: ( 1 )
2: ( 1 2 ) ( 2 )( 1 )
5: ( 1 2 3 ) ( 32 )( 1 ) ( 31 )( 2 ) ( 21 )( 3 )
( 3 )( 2 )( 1 )
15: ( 1 2 3 4 ) ( 4 3 2 )( 1 ) ( 4 3 1 )( 2 ) ( 4 2 1 )( 3 )
( 3 2 1 )( 4 ) ( 4 3 )( 2 1 ) ( 4 3 )( 2 )( 1 )
( 4 2 )( 3 1 ) ( 4 2 )( 3 )( 1 ) ( 4 1 )( 3 2 )
( 4 1 )( 3 )( 2 ) ( 3 2 )( 4 )( 1 ) ( 3 1 )( 4 )( 2 )
( 2 1 )( 4 )( 3 ) ( 4 )( 3 )( 2 )( 1 )
If the urns are distinguishable, then we get the so-called ordered Bell numbers. If the balls and urns are both indistinguishable, we get the partition numbers. The Bell numbers are also related to the Catalan numbers.
The set of combinations is equivalent to what is happening in the 52 different patterns of genjiko. In this traditional Japanese game, 5 incense sticks are selected at random from a supply that includes 5 varieties. The sticks are laid vertically side-by-side and lit; the player then draws a diagram of five vertical lines, and connects the tops of any lines that are found to be the same.
The Bell numbers can be generated by the following table, which works kind of like Pascal's Triangle. Write the known terms of the sequence across the top, and add together, for example 7+20=27, and at the bottom you will get the next term in the series:
|
Number of weeks per year, on average, by the Gregorian calendar (see 365.2425). 365-day years have 52 1/7 weeks, leap years have 52 2/7.
53 is 2×33-1. It is possible to arrange all the natural numbers into a sequence of fractions like this:
(1+2)/3
(4+5+6+7+8+9+10+11)/12
(13+14+15+ ... +36+37+38)/39
(40+41+42+ ... +118+119)/120
...
so that each fraction is a whole number. When this is done, the denominators are all numbers of the form (3n-3)/2, and the fractions are of the form 2×3n-1: 1, 5, 17, 53, 161, 485, 1457, 4373, 13121, 39365, 118097, 354293, 1062881, 3188645, 9565937, 28697813, 86093441, ... (Sloane's A48473; my MCS125664)
54 is the number of coloured squares on a Rubik's CubeTM or on similar toys and puzzles that take the form of a cube with 3×3 pattern on each face. This is also twice the number of "little cubes" (33×2) but that is just a coincidence.
The number that most Americans know best from its use as a speed limit also happens to be a Fibonacci number and the sum of the numbers 1 through 10 (which makes it the 10th triangular number). There are no larger numbers that are both a Fibonacci and triangular.
55 is also 52+42+32+22+12. Such numbers are called pyramidal numbers, because you can stack the squares on top of each other (with the largest on the bottom) to make a pyramid. Sometimes they are called square pyramidal numbers to distinguish them from the tetrahedral numbers. You can add the next square to each pyramidal number to get the next pyramidal number. The pyramidal numbers are: 1, 5, 14, 30, 55, 91, 140, 204, 285, 385, 506, 650, 819, 1015, 1240, 1496, 1785, 2109, 2470, 2870, 3311, 3795, 4324, 4900, 5525, ... (Sloane's A0330; my MCS1936). 4900 is a particularly special one because it is itself a square, see that article for more.
Another way to express the sum of squares above is: 5×5+4×4+3×3+2×2+1×1. If you change the + and × in that expression to × and exponents respectively, you get 86400000, the number of milliseconds in a day.
(partition numbers)
56 is one of the partition numbers, which count the number of ways of placing N indistinguishable balls into one or more indistinguishable urns (but with no empty urns). For example:
1: (*)
2: (**) (*)(*)
3: (***) (**)(*) (*)(*)(*)
5: (****) (***)(*) (**)(**) (**)(*)(*)
(*)(*)(*)(*)
7: (*****) (****)(*) (***)(**)
(***)(*)(*) (**)(**)(*) (**)(*)(*)(*)
(*)(*)(*)(*)(*)
11: (******) (*****)(*) (****)(**)
(****)(*)(*) (***)(***) (***)(**)(*)
(***)(*)(*)(*) (**)(**)(**) (**)(**)(*)(*)
(**)(*)(*)(*)(*) (*)(*)(*)(*)(*)(*)
The sequence runs: 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, 135, 176, 231, 297, 385, 490, 627, 792, 1002, 1255, 1575, 1958, 2436, 3010, ... (OEIS sequence A0041, more terms there).
If the urns are distinguishable, then we get the powers of two. If the balls are distinguishable, we get the Bell numbers.
There are 161280 ways to arrange the digits 1 through 5 in a 5×5 square so that each digit appears once in each row and once in each column. Such an arrangement is called a latin square. If the first row has its digits in increasing order, it is called a reduced latin square. There are 56 5×5 reduced latin squares. Here is an example:
1 2 3 4 5
2 3 5 1 4
3 5 4 2 1
4 1 2 5 3
5 4 1 3 2
9×9 latin squares are familiar to anyone who has played sudoku.
This is the value of x for which xx=10100. It is therefore the biggest number you can raise to its own power on most scientific calculators.22 See also 2.506184... and 69.
(Leyland numbers)
57 can be expressed as a sum xy + yx where x and y are integers greater than 1 — in this case, 25+52=57. Such numbers are called Leyland numbers; the sequence begins: 8, 17, 32, 54, 57, 100, 145, 177, 320, 368, 512, 593, 945, 1124, 1649, 2169, 2530, 4240, 5392, 6250, 7073, 8361, ... (Sloane's A76980. Here is a table showing the 22 Leyland numbers less than 10000:
|
See also 5.19344...×1015070.
By the Aperiodical's study (see 51), this is the second-most-often-mistakenly-thought-to-be-prime number. It is also associated with mathematician Alexander Grothendieck, well-known for thinking abstractly, in a story claiming that he offered 57 as an example of a prime number, perhaps because actually knowing that it's not prime was too concrete.
58 is the sum of the first 7 primes: 2+3+5+7+11+13+17=58. The sequence you get by starting with 2 and adding each prime in succession is: 2, 5, 10, 17, 28, 41, 58, 77, 100, 129, 160, 197, 238, 281, ... (Sloane's A7504). This sequence grows a little faster than the triangular numbers: for arbitrarily high n, the nth number is about n2×log(n)/2.
First page . . . Back to page 6 . . . Forward to page 8 . . . Last page (page 25)
Quick index: if you're looking for a specific number, start with whichever of these is closest: 0.065988... 1 1.618033... 3.141592... 4 12 16 21 24 29 39 46 52 64 68 89 107 137.03599... 158 231 256 365 616 714 1024 1729 4181 10080 45360 262144 1969920 73939133 4294967297 5×1011 1018 5.4×1027 1040 5.21...×1078 1.29...×10865 1040000 109152051 101036 101010100 — — footnotes Also, check out my large numbers and integer sequences pages.
 s.30
s.30