Notable Properties of Specific Numbers
First page . . . Back to page 15 . . . Forward to page 17 . . . Last page (page 25)
(2x2x2 Rubik's cube)
The number of ways to arrange a 2×2×2 Rubik's Cube (where whole-cube rotations and reflections are considered equivalent).
As there are no centre cubelets to determine the orientation, one corner is considered to have a fixed, defined location and orientation (for example, the red-yellow-blue corner is always kept in the top-left-front position with blue on top and yellow on the front). The other 7 can be put into any of the 7!=5040 possible positions, and six of those can be rotated into any of 3 different rotations (the last one's rotation is then determined, as the total rotation of all 8 pieces always adds up to 360o).
See also 4.3252...×1019, 7.40119...×1045, 2.8287...×1074, 1.5715...×10116, and 1.95005...×10160.
One in a series of crossover points in the level-index representation for numbers proposed by Lozier and Turner.
According to early Hindu mythology, the mahayuga or "great age" is a period of time consisting of four consecutive ages, lasting 1728000, 1296000, 864000 and 432000 years for a total of 4320000. They placed themselves and all of humanity in the fourth of these ages, see 432000. The great age repeats many times; the longer periods in the Hindu cosmological calendar are described under 622080000000000. See also 8640000000.
This is 97 and is also the sum of 274 and 1623. See also 512.
This is the "original" Smith number, and was in fact the telephone number of someone named Smith. A Smith number is a number for which the sum of the digits is equal to the sum of the digits of its prime factors: 4937775 = 3×5×5×65837, and 4+9+3+7+7+7+5 = 3+5+5+6+5+8+3+7. Numberphile has a video on it: 4937775 - Smith numbers. See also 22 and 1×1010694985.
This number when displayed on a calculator with 7-segment display, spells "BOOBIES" when viewed upside-down. It is sometimes said to be the first widely-known example of Calculator spelling, though 0.7734 is perhaps more credible. See also 176, 7702219, and 71077345.
A term in the Ramanujan α-series, defined on page 82 of Ramanujan's "Lost notebook". See 336365328016955757248 for details.
A term in the Ramanujan β-series, defined on page 82 of Ramanujan's "Lost notebook". See 336365328016955757248 for details.
The length (in metres) of the major (transverse) axis of the ellipsoid (or oblate spheroid) used by the WGS 84 model to approximate the shape of the Earth. This is very close to the average equatorial radius of the Earth, if you measure based on where the gravitational field is equal to that at sea level. (The sea, being a fluid, tends to equalise its height profile such that gravity is the same at all points on its surface, and the WGS 84 model is calibrated to agree with sea level as closely as possible). See the Geoid article for an explanation of how the geoid (the "gravitational equipotential surface") differs from the actual surface of the Earth. Apart from following the sea height as just mentioned, it tends to be underground below any significantly elevated land. Local changes of density in the mantle and crust add lots of variation.
If the earth were a sphere and the meter agreed exactly with its original definition, this would be exactly 20 million divided by pi.
See also 298.257223563 and 20003931.4585.
This number is an exceptional counterexample to the abc conjecture. The abc conjecture states that, given two relatively prime numbers a and b, the sum of the distinct prime factors of a, b and of their sum c=a+b, called rad(abc), is "almost always" bigger than c. For example when a=7 and b=33=27, c=34=2×17, which makes rad(abc)=2×3×7×17=714, quite a bit bigger than c. 6436343 is special because it is so far in the other direction: a=310×109, b=2, c=235=6436343, and rad(abc)=2×3×23×109=15042, much less than c.
A term in the Ramanujan γ-series, defined on page 82 of Ramanujan's "Lost notebook". See 336365328016955757248 for details.
7129199 = 7×112×19×443, the first of a Ruth-Aaron pair in which neither number is squarefree. It is the smallest such number, i.e. the first in OEIS sequence A178214.
7129200 = 24×3×52×13×457, the second of a Ruth-Aaron pair.
The number of demons, often attributed to Talmudic tradition: 1111 legions of 6666 demons each. See also 666, 44435622, 133306668, 399920004, and 1758064176.
A prime number made from consecutive digits (rearranged). This number and 2143 are the only two ways to make a prime number from consecutive digits. Other numbers of digits do not work, because for example 1+2+3+4+5 is a multiple of three and therefore any arrangement of these five digits will also be a multiple of three. Thus there is no 10-digit "pandigital prime". See also 3816547290 and 10123457689..
When written in the UK style (horizontal strokes through the 7's, and a straight, not curved, vertical stroke for the 9) and held up to a mirror, this number looks fairly like "PISS OFF". See also 176, 22024, and 5318008
8114118 is a palindrome, and the 8114118th prime 143787341 is also a palindrome. This is the smallest such number, after a few early trivial cases (like 11 which is the 5th prime). The prime is a member of A46941 and its index is in A46942. It was discovered by Carlos Rivera35, and is followed by 535252535.
The first counterexample to the classical conjecture that any number of the form 2P-1(2P-1), with P prime, is perfect. See 2047 and 496.
The digits of the most iconic phone number in the history of 1980's one-hit wonders. "867-5309/Jenny" was recorded by pop band Tommy Tutone in 1981 and was on the charts for some months thereafter. For the xkcd version and a cool bonus, see 867.5309....
See also 525600, 10000000000, 0118 999 881 999 119 725 3, and 101010.
This is both a prime and a palindrome, the next-larger palindrome prime is 9136319. This would not be very special if it were not also for the fact that, in the digits of π, the digits 9136319 appear starting at position 9128219.
See also 7427466391.
Lesser-known complement to the well-known 1024, this large power of 5 is hardly ever used but is exactly as close to a crore as 1024 is to 1000; and of course their product is exactly 10 billion. See also 3125.
The first of a set of 5 consecutive primes that are spaced an equal distance apart: 9843019, 9843049, 9843079, 9843109 and 9843139 are all prime, there are no primes in between, and the spacing between each one and the next is 30. 9843019 is the lowest number with this property; the next is 37772429. See also 47, 251, 121174811 and 19252884016114523644357039386451.
107 appears in the definition of the vacuum permeability constant μ0, also called the "permeability of free space", in the curious formula:
μ0 = 4π/107 N/A2
where N is newtons and A is Amperes. Those are both long-established units in the SI system, so one might wonder where this 107 comes from.
A current formal definition of the ampere is "the constant current which will produce an attractive force of 2×10-7 newtons per metre of length between two straight, parallel conductors of infinite length and negligible circular cross section placed one metre apart in a vacuum". There is that factor of 107 again, right in the definition of the ampere. Persuing this further goes right back to the definition of μ0, a circular definition.
To reveal the origin of the 107 we have to look at the history of the ampere unit and the discovery of the force between two electric wires carrying current, a phenomenon first demonstrated by Andre-Marie Ampere in 1820. The (historical) original definition of the modern unit is 1/10 of the unit now called an abampere, which in turn was "the amount of current which generates a force of two dynes per centimetre of length between two wires one centimetre apart". A dyne is a g cm/s2, and a newton is a kg m/s2, so a dyne is 10-5 newtons. In the units that were common in Ampère's time, μ0 was simply 4π:
μ0 = (4π/107) N / A2
= (4π N) / (107 A2)
= (4π 105 dyne) / (107 (abampere/10)2)
= (4π dyne) / (102 (abampere/10)2)
= 4π dyne / abampere2
So we see that the 107 in the modern definition of μ0 is a relic of the old centimetre gram second system of units. Converting from dynes to newtons diminished the value by 105; measuring the force per meter of wire rather than per centimeter increased the value by 102; moving the wires from a distance of 1 cm to 1 meter canceled that 102 out, and measuring the current in amperes rather than abamperes reduced the force by 102 because Ampère's force is proportional to the product of the currents in the two wires and both measurements change by a factor of 10 (the number of amperes in an abampere).
107=1,00,00,000 is a unit of the Indian number name system. It is called crore in written English, though in Iranian usage a crore is 500000. See also 10000 and 100000.
This is π④e, where ④ is the higher-valued form of the hyper4 operator, using my (somewhat arbitrary and speculative) generalisation of tetration to real arguments based on the error function erf(x)). See also πe, 3581.875516... and 4341201053.37.
12833424 = 73.2×365.25×24×2/3×30
Tony Padilla's estimate of the number of times a person thinks of a number during their "waking life". The derivation is based on an average life-span of 73.2 years, multiplied by 365.25, 24 (hours in a day), 2/3 (the fraction of one's time that one is awake), and 30 (based on the notion that people think of numbers an average of once every two minutes).
See also 1.5×1020.
A constant appearing in the Chudnovsky series approximation of pi.
See 210691031040000.
This is 224 and is equal to 2503+1003+503+303+63. Since all of those cubes except 63 end in 000, 216 shows up all by itself at the end of the number. See also 246924, 2097152 and 134217728.
A product of two non-overlapping sets of consecutive integers: 17297280 = 8×9×10×11×12×13×14 = 23×32×2×5×11×22×3×13×2×7 = 2×3×7×26×5×13×6×11 = 63×64×65×66. This type of match is is more "unlikely" than that demonstrated by 19958400 because it requires more prime factors to work out right after rearranging. See also 720, 175560, and Sequence A064224.
Combined fuel economy of a Toyota Prius, in SI units (50 miles per gallon converted to meters (of distance traveled) per cubic meter (volume of fuel consumed)). See xkcd 687 and 3.1418708596056; see also 137.035.
19958400 = 3 × 4 × (5×6×7×8×9×10×11) = (5×6×7×8×9×10×11) × 12 = 12! / 24. This is the product of the integers 3 through 11, and also the product of integers 5 through 12. There are an infinite number of ways to construct a number with this sort of pattern, all of which have a similar form: two consecutive numbers at the beginning (in this example 3×4) get replaced by their product, an oblong number (in this example 12), at the end. The general form is:
n×(n+1)×(n+2)×...×(n2+n-2)×(n2+n-1) = (n+2)×...×(n2+n-2)×(n2+n-1)×(n2+n) = (n2+n)!/(n+1)!
The sequence grows about as quickly as the factorials of the squares: 120, 19958400, 20274183401472000, 368406749739154248105984000000, ...
See also 17297280 and Sequence A064224.
The length (in meters) of the IUGC standard meridian. This represents the length of a line from one pole of the Earth to the other (crossing the equator midway, i.e. at about the 10,002-kilometer point). It is an international standard agreement, and is a sort of average of meridians at different longitudes75. The original definition of meter was based on the meridian and would have had this number be exactly 20000000. The original determination of the meter's length, based a massive seven-year surveying project, established a meridian length that was too small.
Later improvements in understanding about the Earth's shape and extensive established use of the meter for non-surveying purposes made it necessary for the unit to diverge from its original meridian-based definition. The total change in length of the meter through this process was about 195 parts per million. The meter ended up being a bit "shorter", and the initial meridian measurement was too short (by a greater amount), so the average meridian is now known to be nearly 20,004 km. See also 1852.
The largest prime number with consecutive increasing digits. See also 4567.
The price in US dollars for a used book ("The Making of a Fly" by Peter Lawrence) that was briefly offered on Amazon by two rival used book sellers, after several weeks of automatic algorithmic adjustment. The price escalated in repeated steps, each following a similar pattern: Seller A's algorithm checked once per day for any change in seller B's price, responding by adjusting its own price to always be undercutting B by a factor of 0.9983; later in the day B's algorithm did something similar but aimed to always charge 1.270589 times as much as A. Both strategies, taken individually, are plausible (B's aim-high strategy makes sense if B has a higher seller rating or a loyal customer base). Unfortunately for both, no stable price is possible because only the seller who made the most recent price adjustment will be "satisfied" with the situation. A's and B's prices increased by a factor of about 1.2684 = 1.270589×0.9983 per day. This continued for about 7 or 8 weeks, the time needed to rise from a reasonable level for this title (about $20.00 when I checked) to the $23 million high. As related by Matt Parker, the price was 1730045.91 at the time that a real person (a genetic scientist) first noticed the problem.
The number of seconds in common (non-leap) year: 365×86400. Although Leap seconds are called "intercalary", they are effectively part of the year because the leap second occurs during the day, local time (for example, in a time zone 7 hours away from UTC, the clocks would go from "16:59:59" to "16:59:60" to "17:00:00") so a common year with a leap second would be 31536001 seconds long.
See also 432000, 604800, 31556952 and 31622400.
The number of SI seconds in a tropical year, according to xkcd 1061. The "Earth Standard Time" system, which is "simple, clearly defined, and unambiguous", defines a year by the following rules:
1 year = 12 months; 1 month = 30 days; 1 day = 1440 minutes (= 24
hours 4 minutes); 1 minute = 60 SI seconds. This gives 1 year =
31190400 SI seconds.
For 4 hours every full moon, run clocks backward. Full moons
happen every synodic month, which is 29.530588853×86400.001 =
2551442.9... SI seconds. After going backwards for 4 hours, the clocks
have to go 4 hours forward before continuing, so 8 hours = 8×3600 = 28800
seconds will be added. This increases the average length of a year by
a ratio of (2551442.9...+28800)/2551442.9... = 1.01128773..., making it
31542468.8... SI seconds.
The non-prime-numbered minutes of the first full non-reversed
hour after a solstice or equinox happen twice. The 17th prime number
is 59, so there are 43 non-prime minutes in an hour. There are two solstices
and two equinoxes per year, so this rule adds 43×60×4 = 10320 seconds
to the year, for a year of 31552788.8... SI seconds.
31556925.6... = 365.242189670 × 86400.001
An approximation of the number of SI seconds in a mean tropical year, as experienced during the years 1995-2012. This is based on the average rate of rotation of the Earth during that period (see mean solar day) combined with the tropical year length for the year 2000 (which is in mean solar days). The figure for the length of the mean solar day has less precision because of the variations in Earth rotation rate on short timescales49,125, due to weather and ocean currents, etc. whereas the year length figure represents an average over a period of several years.
The approximation to the number of seconds in a mean tropical year used in the 1956 and 1960 definitions of the SI second :
the fraction 1/31,556,925.9747 of the tropical year for 1900 January 0 at 12 hours ephemeris time.
This number is related to Newcomb's solar motion coefficient as:
31556925.9747 × 129602768.13 = 36525×86400 × 360×60×60
In words, the number of SI seconds in the mean tropical year multiplied by the Sun's mean rate of motion in arc-seconds per century is equal to the number of seconds in a Julian century times the number of arc-seconds in a full circle.
See also 129602768.13.
This is the number of seconds per year according to the Gregorian calendar (averaged over a 400-year period): 365.2425 times 86400. It is an exact integer but is just an average; the number of seconds in any particular year is always either 31536000 or 31622400.
Randall Munroe[226] found the approximation 754=31640625, which is a better approximation than the popular (among physicists) π×107 = 31415926.535... .
Number of seconds in a Julian year (often used in astronomical ephimerides, for things like proper motion of stars, orbital elements of planets, etc.).
The number of seconds in a leap year: 366×86400. Although Leap seconds are called "intercalary", they are effectively part of the year because the leap second occurs during the day, local time (for example, in a time zone 7 hours away from UTC, the clocks would go from "16:59:59" to "16:59:60" to "17:00:00") so a leap year with a leap second would be 31622401 seconds long.
See also 432000, 604800, 31536000 and 31556952.
The last in a sequence of similar-looking prime numbers: 31, 331, 3331, ... are prime51. The following number in the series is not: 333333331=17×19607843. See also 73939133.
See 1001.
The largest triangular number of the form T(x2-1) that is also 6 times another triangular number; see 91.
A textbook on GIS systems for environmental modeling 129 contains a discussion of the problem of dealing with "liguistic hedges" (words and phrases such as acceptable and not terribly certain) for purposes of data entry and database lookup. They contemplate converting back and forth between such words/phrases and "fuzzy sets" of quantitative values (statistical distributions on the interval [0..1]). The general idea is that each word or phrase can be mapped onto a statistical distribution: for example, "above average" might correspond to a bell-curve-shaped distribution that is nonzero between 0.5 and 0.8 with a peak at 0.65. They suggest that converting the other way (from statistics to representative words) could be done with a database that maps groups of fuzzy sets onto groups of words/phrases. they dismiss this can be difficult:
"Not only is the notation difficult to encode, but there are 39,916,789 useful combinations of fuzzy sets in the range [0,1] for an interval of xi = 0.1."
The number cited here is 11!-11, the McCombinations of 11. Though it is clear how to define 11 fuzzy sets with peaks from 0.0 to 1.0 spaced 0.1 apart from each other, one may wish to speculate on how the author thought that 11! was relevant to the problem, and why they deemed it necessary to subtract 11.
A "self-describing" number, like 3211000 and 521001000; see 6210001000 for more.
This is the number of demons in hell, as calculated by Johann Weyer (also spelled Wierus) and described in his 1583 book Pseudomonarchia Daemonum. The number is based on 6666 "legions" with 6666 demons each, all governed by 66 rulers similar to those in the Ars Goetia section of a mid-1600s spellbook Lemegeton Clavicula Salomonis. There are many versions of this, resulting in different numbers of legions, etc. See also 666, 7405926, 133306668, 399920004, and 1758064176.
The maximum number of steps a 5-state, 5-tuple Turing machine can make, on an initially blank tape, before halting. This is called the "five-state busy beaver BB(5) by the S(n) function". It was found by Buntrock and Marxen in 1989, and is listed in this paper where it is described as "current BB(5), step champion". See 107 for more.
This is the number of different ways that one can visit the state capitols of the 48 contiguous states in the United States, passing through each state only once. The same route in reverse does not count as a distinct route, and one end of the trip must be in Maine because it only borders one other state. The answer, and a description of algorithms used to calculate it, are in Knuth [169] section 7.1.4 (Binary Decision Diagrams), (p. 255 in the 2011 edition).
See also 25623183458304.
Type this on a calculator and read the display upside-down; it (sort of) says "SHELL OIL":


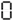


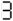
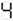
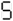 →
→
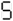
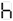
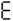


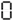


In the 1970's there were a bunch of joke "word problems" that instructed the reader to enter some sort of formula (example: 30 × 773 × 613 - 1 = × 5 =) to produce an answer that is read as a word by holding the calculator upside-down. For this purpose the digits 0,1,2,3,4,5,7,8,9 were used to represent O, I, Z, E, H, S, L, B and G respectively, so the answer/punchline could be any word or phrase using only these letters. See also 31337 and 5318008.
The "Tyson Code", better known as 0073735963 or 007-373-5963, a cheat code in the Nintendo videogame Mike Tyson's Punch-Out that takes the player directly to the final match against Tyson himself. See also 573, 9001, and 1597463007.
This number is prime, and if you take one or more digits off the end, the resulting numbers 7393913, 739391, ... 73, 7 are all prime. This is the largest number with this property. See also 33333331, 381654729, 357686312646216567629137 and 3608528850368400786036725.
(5 hyperfactorial)
The number of milliseconds in a day: 86400000 = 24×60×60×1000. See also 10080, 40320, 432000 and 3628800.
The fifth hyperfactorial: 86400000 = 55×44×33×22×11. See also 55.
It seems rather odd that such a large number is listed for two unrelated properties, but there are larger examples (see 18446744073709551615).
This is the smallest (positive) integer expressible as the sum of two (positive) cubes in three different ways: 1673+4363 = 2283+4233 = 2553+4143 = 87539319. See also 1729.
An astronomical unit in miles, calculated using the IAU definition of the former. The approximation "93 million miles" was commonly taught in the US. This number is precisely defined by agreement, see here for details. See also light year.
A myriad myriad, and the largest number mentioned in the Bible (Hebrew תנ"ך (Tanakh) or Christian Old Testament): Daniel 7:10, "... and ten thousand times ten thousand stood before him, ..." (King James version). It is probably not a coincidence that 108 was also the largest number for which the Greeks had a name; the book of Daniel reached its final form well after Alexander conquered the entire Levant region. See also 666.
108 is 億 in China (yì, dàng) and Japan (oku), where they construct numerals on the basis of 10, 100, 10000, 108, and higher powers of 104. This system closely resembles the Knuth -yllion naming system for very large powers of 10. (See also my list of large numbers in Japanese)
The number of DNA base pairs in the genome of the nematode worm C. elegans. See 959.
The first of a set of 6 consecutive primes that are spaced an equal distance apart: 121174811, 121174841, 121174871, 121174901, 121174931 and 121174961 are all prime, there are no primes in between, and the spacing between each one and the next is 30. 121174811 is the lowest number with this property; it was first discovered in 1967 by L. J. Lander & T. R. Parkin. Along with 2, 3, 251 and 9843019, forms a sequence (Sloane's A6560) that is thought to be infinite, but it is very hard to discover the next one. No one has yet discovered the first set of 7 consecutive primes; such a set would have to have a spacing of 210 or a multiple of 210; see 19252884016114523644357039386451. See also 47, 251 and 9843019.
129600000 = 100 × 360 × 60 × 60.
Number of arc-seconds in a circle times 100. See 129602768.13.
Newcomb's coefficient giving the average rate of motion of the Sun across the sky (or equivalently, the rate of Earth's motion in its orbit, relative to the stars) in units of arc-seconds per century. One might think this number should just be 129600000, but the Earth's axial precession and other effects prevent this.
See also 31556925.9747.
The number of "demons" in hell, as calculated by Alonso de Espina (see 399920004) and based on the notion that 1/3 of them were the fallen angels who thus became demons: 3×6666×6666. See also 7405926, 44435622, and 1758064176.
This number, 227 or 233, is equal to this rather memorable sum of cubes: 5003+2003+1003+603+123. Another way to express this fact is:
ln((5322)3 + (5223)3 + (5222)3 + (3×4×5)3 + (3+4+5)3) = ln(2) 33
Scary but true: I actually discovered and verified this property of 227 by doing the math in my head. I already knew most of the powers of 2 up to 224=16777216. And, like tens of other kids around the world, I learned the squares up to 202 and the cubes up to 123 in grade school. One day I decided to double 224 a few times to get 227, then noticed the 217728, which looks a lot like 216 and 1728 stuck together. It was then fairly easy to see the rest, since 134 is 125 plus 8 plus 1. See also 2097152.
See also 151115727451828646838272.
This is a 9-digit number containing each of the digits 1 through 9, and equal to the sum 96+89+73+62+57+44+31+25+18, in which each of the digits occurs exactly once as a base and exactly once as an exponent. Inder J. Tenaja calls numbers of this type "flexible power selfie numbers", and found a total of 25 of them (with 389645271 being the largest).
The astronomical unit in kilometers, based on the IAU definition of the former. See also 149597870691.
This number figures in an approximation of π that makes a puzzling appearance in the result (on certain calculators) of computing 116/13. The "approximation of π" in this case is (116×3600)/(13×156158413) = 3.14159265358903895... Matt Parker has a video on this. The reason for the calculator presenting this answer is an unsolved mystery. This is not that great an approximation considering how much is on the left-hand side: 18 digits and some symbols to get 13 digits of π. (RIES can do much better, admittedly not as a rational number, but we have continued fractions for that).
The number of integer partitions of 100, if identical parts are allowed. This is the more well-known version of the "partition numbers" is Sloane's A0041, starting: 1, 1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, 135, 176, 231, 297, 385, 490, 627, ... For example there are 15 ways to make a sum equal to 7: 7, 6+1, 5+2, 5+1+1, 4+3, 4+2+1, 4+1+1+1, 3+3+1, 3+2+2, 3+2+1+1, 3+1+1+1+1, 2+2+2+1, 2+2+1+1+1, 2+1+1+1+1+1, and 1+1+1+1+1+1+1.
See also 444793.
In early 2009, one David Horvitz (an artist who enjoys posting unusual ideas on his blog) suggested that people should take a photo of themselves standing in front of a fridge or freezer with the door open and their head in the freezer, then share it online (e.g. with Instagram or Flickr) tagged with the number 241543903. The idea caught on (becoming an internet meme) and an image search for this number will now return dozens of such photos.
See also 3112066128.
This number has 1008 distinct factors, and is the smallest number with at least 1000 factors. Its prime factorisation is 26×32×52×7×11×13×17. See also 12, 840, 1260, 10080, 45360, 720720, 3603600, 278914005382139703576000, 2054221614063184107682218077003539824552559296000 and 457936×10917.
270270271 is prime, and is known to be a factor of 1010100+27. This seemingly amazing fact is actually quite easy to prove, using power-tower modulo reduction. Alpern 94 lists many such factors.
The smallest 9-digit number that, when written in three rows of 3 (as in one block of a Sudoku puzzle) forms a 3×3 magic square. There are 7 others: 294753618, 438951276, 492357816, 618753294, 672159834, 816357492, and 834159672.
299128000
An approximation to the speed of light hypothesised to be in Sayana's commentary on the Rigveda; see 2202 for details. See also 309467700.0.
(the speed of light)
and the definition of the meter (length unit)
299792458 is the speed of light in meters per second. In 1983 by international agreement, the meter was redefined in terms of the speed of light, and as a result the constant for the speed of light is now exactly 299792458 meters per second. The second, in turn, is defined as precisely 9192631770 times the frequency of photons in a Caesium maser-based atomic clock. See also 2.54, 8.987552×1016, 1.616×10-35 and 5.391×10-44.
The speed of light was first calculated from astronomical measurements in 1710 by Ole Romer, but had to be expressed as a ratio to the speed of Earth in its orbit (or equivalently, in terms of certain unknown Solar System distances and known light travel times) because the size of the astronomical unit had not yet been determined to sufficient accuracy; this would not come until the late 1700's (see 149597870691 for more).
A meter is also just about equal to the length of a pendulum with a period of precisely two seconds (a seconds pendulum, the length is close to 994 millimeters). In fact, this definition was proposed as the standard unit of length over 100 years before the original Metric system became official, and for most of the 18th century it was one of two competing proposals. The other proposal (based on the size of the Earth) was chosen because the period of a pendulum depends on where it is measured. (See 20003931.4585 for more about the meridian measurement and its errors).
It is a strange coincidence that the gravitational acceleration at Earth's surface (9.8 meters per second2) times the length of Earth's year (about 31557600 seconds) is about 310000000 meters per second, just a little bit bigger than the speed of light. There is no significance to this coincidence, it's just kind of cool. See also 3.14187.
See also 186282.397.
The mean acceleration due to gravity on the Earth's surface, times the number of seconds in a mean tropical year. This happens to be only a few percent larger than the speed of light. This serves as a guideline to some basic limits on long-duration manned space flight. Since astronauts would probably need to experience no more than about 1.1 or 1.2 times normal gravity during their trip, it would take a few years (even from the astronaut's own relativistic frame of reference) to make the trip even to the nearest stars.
This is the smallest number that can be expressed as a×ba in three distinct ways: 344373768 = 8×98 = 3×4863 = 2×131222. See also 648.
The Mahler-Popken complexity metric (a sort of Kolmogorov complexity) counts how many 1's it takes to create an expression with a certain integer value, using just addition and multiplication (and parentheses); see OEIS sequence A5245. For example MP(7)=6 because 7=(1+1)×(1+1+1)+1, which uses 6 1's R.K. Guy conjectured that for any prime p, MP(p)=1+MP(p-1). This turns out to be false, the first counterexample being the prime 353942783: it is the sum of two composites, 2×3+37×9566021, which together add up to a complexity score of 63, the same as 353942782 = 18379×19258. Domotro has made a great video about the Mahler-Popken metric.
Polydivisible numbers
This 9-digit number contains one each of the digits 1 through 9, and has the additional property that the first two digits (38) are a multiple of 2, the first 3 digits (381) are a multiple of 3, and so on up to the whole thing being a multiple of 9. You can see a bit of symmetry in the digits: the first three digits (381) plus the last 3 (729) add up to 10×111, and the middle 3 (654) plus itself in reverse (456) also adds up to 10×111. This type of number is called polydivisible, and this one is also pandigital in that it contains each digit (except 0) exactly once. There are lots of such numbers if you don't care about having one each of the digits 1 through 9. See also 3816547290, 30000600003, and 3608528850368400786036725.
This is the largest number you can express with just two digits and possibly one symbol (99, 9 ^ 9 or 9③9). See also 4.28...×10369693099 and 101.0979×1019.
389645271 = 99+87+76+62+55+44+38+21+13
See 134827965.
The number of angels as calculated by Alonso de Espina in his book Fortalitium Fidei, according to the derivation: 9 orders (or "choirs") of angels (according to Pseudo-Dionysius the Areopagite) each consisting of 6666 legions, each containing 6666 individuals: 9×6666×6666 = 399920004. See also 7405926, 44435622, 133306668, and 1758064176.
This is Hω2+ω*2+2(4) and Hω2*2(3), where Hn() represents the n-indexed function in the Hardy hierarchy, one of the function hierarchies that arise in the study of large numbers and how to name them. See 402653211 for more.
This number appears in the value of G(4), where G(n) represents the "base" in the Goodstein's Theorem iteration when the Goodstein sequence iteration ("strong" variant) reaches the value zero: G(4) = 3×2402653211 - 2. See that number for more.
456790123 has the "370-property": it is equal to the average of all possible permutations of its digits. Since there are 9 digits, there are 9! = 362880 permutations. That would take a really long time to add up to take an average, but we can save a lot of work by noting that each digit occurs in each position an equal number of times. For example, the digit "4" will appear in each position in exactly 1/9 of the permutations. This effectively means that we can compute the average much more quickly just by using one representative permutation with each digit in each possible position. In this case, that can be done by computing:
(456790123 + 567901234 + 679012345 + 790123456 + 901234567 + 012345679 + 123456790 + 234567901 + 345679012) / 9
where the 9 terms are the original number rotated into all possible positions (like the multiples of 142857). If you take this sum (on a 10-digit calculator) you'll find that the average is equal to the original number, 456790123. These numbers of this type (first pointed out to me by reader Claudio Meller) are discussed more fully on their own page.
A "self-describing" number, like 1210 and 42101000; see 6210001000 for more.
535252535 is a palindrome, and the 535252535th prime 11853735811 is also a palindrome. This is similar to 8114118 and was discovered by Giovanni Resta. The prime is a member of A46941 and its index is in A46942 35
This is a power of 2, and a 9-digit number in which all 9 digits are different. There is no 10-digit power of an integer in which each of the digits 0 through 9 appears once. See also 295147905179352825856.
A constant appearing in the Chudnovsky series approximation of pi.
Length of Earth's orbit in miles, based on this definition of the astronomical unit.
See also 939951143167.59.
The smallest number expressible as the sum of two 4th powers in two different ways: 635318657 = 594+1584 = 1334+1344. It is sometimes called a Generalized taxicab number because of its shared property with 1729. See also 50, 65, 1729, and 588522607645608.
The (false) Polya conjecture stated that positive integers with an odd number of prime factors always outnumber those with an even number of prime factors. In this case, the "number of prime factors" is sequence A001222, in which the same prime can be counted twice (so for example 8=23, 12=22×3 and 30=2×3×5 are all counted as having 3 prime factors). But the conjecture turns out to be false in a small region starting at 906150257 and extending up to 906488079.
See also 1.397162914×10316.
The number of seconds from the 1st January 1970 until the 1st January 2001. This is 11323 days, i.e. (365×31+8)×86400 seconds, because 2001 is 31 years after 1970 and there were 8 leap years during that period. The number appears as an offset in time/date calculations when converting between the UNIX epoch and the epoch used in the MacOS Cocoa framework ("Core Foundation"), and in application that use it (such as sqlite3 running on a Mac). Both epochs use 00:00:00 GMT as the moment the counting starts, and ignore leap seconds. Cocoa defines the constant kCFAbsoluteTimeIntervalSince1970 equal to 978307200.0L
See also 2082844800, 3061152000, and 11644473600.
This is (1000-1)3 = 10003-3×10002+3×1000-1, and its reciprocal 1/997002999 = 0.000000 001 003 006 010 015 021 028 036 045 055... gives us the triangular numbers. This happens because the generating function of that sequence is 1/(x-1)3. For more on this, see my separate article Fractions with Special Digit Sequences; see also 89, 99.9998, 199, 998, 9801, and 9899.
(a short scale billion)
A billion in the short scale system used in the United States, and adopted by the UK and other English-speaking countries in the late 20th century. Many other countries use the short scale but have milliard or a transliteration (such as Arabic milyar) as their name for 109. Other countries and languages (including Afrikaans, Farsi/Persian, most of continental Europe, and countries with earlier history as European colonies) use the "long scale" in which a "billion" is 1012 and a "trillion" is 1018. Those with no Chuquet-derived names at all include the languages of India, China, and Southeast Asia (some examples of non-Chuquet names are at 100000, 107, 1011, 1044, and 1059.)
The difference in meaning of "billion" (109 versus 1012) came into being at a time when it didn't matter to most people. But thanks to many factors (population growth, inflation, prosperity, technology, and education) numbers in the billions are now very common in the news and in everyday speech. The reputation (whether good or bad) associated with the millionaire of the early 1900's now belongs to the billionaire. We often hear of costs and deficits in the billions; many of our computers have billions of bytes of storage capacity and perform billions of operations per second.
109 is an estimate of the processing power (in floating-point operations per second) embodied in a human retina. The retinas perform image processing to detect such things as edge movement and boundary direction. The figure is based on a resolution of roughly 106 pixels, a speed of 10 changes per second, and 100 FLOPs per pixel. See also 1018.
1000000001 = 11×90909091 = 1001×999001
Most of the numbers of the form 10n+1 can be factored in simple and pretty ways; this one happens to have two such factorisations.66 Here are most of the simpler patterns:
form examples
103n+1 1001=11×91 1000001=101×9901
1000000001=1001×999001
1000000000001=10001×99990001
105n+1 100001=11×9091
10000000001=101×99009901
1000000000000001=1001×999000999001
107n+1 10000001=11×909091
100000000000001=101×990099009901
102n+1+1 1001=11×91 100001=11×9091
10000001=11×909091
1000000001=11×90909091
104n+2+1 1000001=101×9901 10000000001=101×99009901
100000000000001=101×990099009901
106n+3+1 1000000001=1001×999001
1000000000000001=1001×999000999001
108n+4+1 1000000000001=10001×99990001
100000000000000000001=10001×9999000099990001
As you can see, there are two different sets of patterns. As long as n is a multiple of an odd number, 10n+1 fits at least one of the patterns. The numbers excluded by this are of the form 102i+1: 11, 101, 10001, 100000001, 10000000000000001, etc. (Sloane's A80176, the "base 10 Fermat numbers"). There is no easy factorisation pattern for them. ([154] pp. 137-138)
See also 1001.
A square in which each digit appears exactly once. (Contributed by Cyril Soler). See also 3816547290, 6210001000, 2504730781961, and 295147905179352825856.
This is the second example in a series of near-misses to Fermat's last theorem discovered by Ramanujan, of which 1729 is the famous first example. 1030301000 is 10103, and is just 1 greater than the sum of 7913 and 8123. See this article and the 336365328016955757248 entry for details.
This is the decimal value of the hexadecimal integer constant 0x5f3759df that comprises the central mystery to the following bit of code, which is mildly famous among bit-bummers and purports to compute the function f(x) = 1/√x:
/* Note: This assumes "int" and "float" are both 32 bits */ float InvSqrt( float x ) { const float k3_2 = 1.5f; // constant 3/2 float x_2 = 0.5f * x; // x/2 (reused a couple times) float y = x; int i = * ( int * ) &y; // evil floating point bit hack i = 0x5f3759df - ( i>>1 ); // Initial approximation (WTF ?!?) y = * ( float * ) &i; y = y * ( k3_2 - ( x_2 * y * y ); // Newton iteration // y = y * ( k3_2 - ( x_2 * y * y ); // Iterate again for full accuracy return y; }This code actually works. It performs four floating-point multiplys, one floating-point add, an integer shift, an integer subtract, and two register moves (FP to Int and Int back to FP). It generates the correct answer for the function to within three decimal places for all valid (non-negative) inputs except infinity and denormals.
The hex value 0x5f3759df is best understood as an IEEE floating-point number, in binary it is 0.10111110.01101110101100111011111. The exponent is 101111102, which is 190 in decimal, representing 2(190-127) which is 263. The mantissa (after adding the hidden or implied leading 1 bit) is 1.011011101011001110111112, which is 1.43243014812469482421875 in decimal. So the magic constant 0x5f3759df is 1.43243014812469482421875×263, which works out to the integer 13211836172961054720, or about 1.3211...×1019. This is (to a first-order approximation) close to the square root of 2127, which is about 1.3043...×1019. The reason that is significant is that exponents in 32-bit IEEE representation are "excess-127". This, combined with the fact that the "exponent.mantissa" floating-point representation crudely approximates a fixed-point representation of the logarithm of the number (with an added offset), means that you can approximate multiplication and division just by adding and subtracting the integer form of floating-point numbers, and take a square root by dividing by two (which is just a right-shift). This only works when the sign is 0 (i.e. for positive floating-point values).
Here are some example values of numbers from 1.0 to 4.0 in IEEE single-precision:
0.10000001.00000000000000000000000 = 4.0
0.10000000.10000000000000000000000 = 3.0
0.10000000.00000000000000000000000 = 2.0
0.01111111.10000000000000000000000 = 1.5
0.01111111.00000000000000000000000 = 1.0
Here I have shown the sign, exponent and mantissa separated by dots. Since the logarithm of 1 is zero, the value for 1.0 (0.01111111.00000000000000000000000) can be treated as the "offset". If you subtract this offset you get these values, which approximate the logarithm of each number:
0.00000010.00000000000000000000000 = 10.02 = 2.0; log2(4)=2
0.00000001.10000000000000000000000 = 1.12 = 1.5; log2(3)≈1.585
0.00000001.00000000000000000000000 = 1.02 = 1.0; log2(2)=1
0.00000000.10000000000000000000000 = 0.12 = 0.5; log2(1.5)≈0.585
0.00000000.00000000000000000000000 = 0.02 = 0.0; log2(1)=0
From this it is easy to see how a right-shift of the value for 4 yields the value for 2, which is exactly the square root of 4, and a right shift of the value for 2 gives the value for 1.5, which is a bit higher than the square root of 2. Over a full range of input values, the right-shift and addition of the magic constant gives a "piecewise linear" approximation of 1/√x.
The constant "0x5f3759df" is most commonly cited as being found in the Q_rsqrt function of "game/code/q_math.c" in the source code of the videogame Quake III. It is attributed to John Carmack, but the same hack appears in several earlier sources going as far back as 1974 PDP-11 UNIX.
David Eberly wrote a paper[180] describing how and why the approximation works.
Chris Lomont[184] followed up with investigation into its origins, getting as far as a claimed credit to Gary Tarolli of Nvidia. He thoroughly analyzes the piecewise linear approximation for odd and even exponents and proposes 0x5f375a86 as being slightly better, and a similar constant 0x5fe6ec85e7de30da for use with 64-bit IEEE double precision.
David Eberly then wrote a longer explanation[215] analyzing the constant 0x5f3759df along with some other candidates (like 0x5f375a86 and 0x5f37642f). It describes efforts to discover why and how this value originally got chosen; with inconclusive results.
An earlier example of code calculating the square root in this way (approximation via a single shift, possibly with an add or subtract, no conditional testing; but with no Newton iteration) was described by Jim Blinn in 1997, where we find the following code: (see [167]).
inline long int AsInteger(float f) { return * (long int *)&f; } inline float AsFloat(long int i) { return *(float *)&i; } const long int OneAsInteger = AsInteger(1.0f); // 0x3F800000 float ASqrt(float x) /* Approximate Square Root */ { int i = (AsInteger(x)>>1) + (OneAsInteger>>1); return AsFloat(i); }with the comment:
This is actually pretty weird. We are shifting the floating-point
parameter — exponent and fraction — right one bit. The low-order bit
of the exponent shifts into the high-order bit of the fraction.
But it works.
- Jim Blinn ([167] page 83)
The same article discusses several similar functions including ones that include one iteration of Newton's method. Here are his inverse square root functions:
float AInverseSqrt(float f) { int i = (OneAsInteger + (OneAsInteger>>1)) - (AsInteger(f)>>1); return AsFloat(i); } float BInverseSqrt(float x) { float y = AInverseSqrt(x); return y*(1.5-.5*x*y*y); }If these are combined together into a single function with the inlines expanded, we get:
// OneAsInteger defined as above, equals 0x3F800000 const long int Magic = OneAsInteger + (OneAsInteger>>1); // 0x5F400000 float BInverseSqrt(float x) { int i = Magic - ((*(long int *)&f) >> 1); float y = *(float *)&i; return y*(1.5-.5*x*y*y); }A much older example is found in the UNIX library sqrt function for the PDP-11, dating back to June 1974 (see [144]):
/ sqrt replaces the f.p. number in fr0 by its square root. newton's method / ... movf fr0,-(sp) asr (sp) add $20100,(sp) movf (sp)+,fr0 /initial guess / ...which is effectively performing an integer right-shift on the 16 high bits of the input value, then adding a constant similar to the constants in the above examples, and putting the result back into a floating-point register before proceeding with the Newton's method calculations. Only the upper part of the mantissa is being shifted, but that's good enough. A man page from Feb 1973 (Third Edition UNIX) suggests that the routine existed as early as then.
See also 573, 9001, and 73735963.
An alternate value (hexadecimal 0x5f375a86) of this magic constant.
Another alternate value (hexadecimal 0x5f37642f) of this magic constant.
The number of demons in hell, by a later version of Johann Weyer's book Pseudomonarchia Daemonum (see 44435622). Here the organisation is 6 legions each with 66 cohorts each with 666 companies each with 6666 members. See also 666, 7405926, 133306668, and 399920004.
4th in the "paperfolding sequence iteration interpreted as a growing sequence of binary numbers"; see 27876.
The Planck energy in Joules (kg-m/s2). The "(22000)" represents an uncertainty range; to ignore this one might simply approximate the number as 1956100000.
See 3.1418708596056 and 137.035.
The number of seconds from the 1st January 1904 until the 1st January 1970. This is 24107 days, i.e. (365×66+17)×86400 seconds, because 1970 is 66 years after 1904 and there were 17 leap years during that period (including 1904 itself). It is the offset between the UNIX epoch and the epoch used in the old "Classic" MacOS; see 978307200 and 3061152000 for more.
This number is associated with the UNIX epoch, which (on 32-bit systems) will "roll over" on 2038 Jan 18th. Numberphile has a video on it here: End of time (2147483647)
See also 49.710269... and 11644473600.
The number of seconds from the 1st January 1904 until the 1st January 2001. This is 35430 days, i.e. (365×97+25)×86400 seconds, because 2001 is 97 years after 1904 and there were 25 leap years during that period (including 1904 itself). The number appears as an offset in time/date calculations when converting between the UNIX epoch and the epoch used in the old "Classic" MacOS. Both use 00:00:00 GMT as the moment the counting starts, and ignore leap seconds. The Cocoa / Core Foundation framework defines the constant kCFAbsoluteTimeIntervalSince1904 equal to 3061152000.0L
See also 978307200, 2082844800, and 11644473600
In late 2014 a Twitter friend and I undertook a challenge to find the smallest (integer, not starting with any 0's) number that does not appear in any Google search results (or, at the very least, try to estimate how many digits it would have). The agreed rules stipulated that we should back up our claim with an actual number that (by demonstration) actually returns zero results from Google Search (with the understanding that, once we revealed our result by e.g. Tweeting it publicly, it would soon lose its non-Google-able-number status).
Using Fermi Estimation (see Randall Munroe's what-if 84), I estimated that: there are 1010 people, each has 1 webpage, each with 1000 words; but only 1% of these are devoted to long lists of unique numbers (like invoice numbers, telephone numbers, etc.), and probably 90% of them are either small and duplicate each other somewhat, or are big and leave gaps. Answer: the smallest integer not indexed by Google is probably 10 digits long.
He and I spent a while trying numbers, and pretty quickly found that the 10-digit numbers seem to be almost all taken. 11-digit examples were easy to find. After just 10 minutes or so we had gotten down to the very low 11 digits (my best was 10826746091, his was 11170063270).
He kept looking for 10-digit numbers, and noticed that there seem to be extensive lists of primes, but not of composites. He discovered that 6255626957 = 109×3803×15091 was unknown to Google, and soon after found that the Marshall Islands have country code +625. (The islands have 7-digit phone numbers but only enough people to use a small fraction of them, thus offering a possible explanation). Shortly after this, he and another had found 3112066128 = 24×3×64834711. (Internationally, +31 is The Netherlands but 9 digits must be added; within the U.S. 311 is an N11 code; so there are no 10-digit telephone numbers starting with 311).
Clearly this number would be indexed soon after appearing on this page (and that indeed happened), so I would call it a "likely upper bound" for whatever number is actually the smallest positive integer not in any Google result. Within a few years (of our contest, i.e. a few years after late 2014), perhaps all 10-digit numbers will have appeared somewhere.
See also 241543903, 1.5×1020, and 1.76×1067.
3432948736 is the smallest number N such that N = 2N mod 10K, where K=10. In other words, 2 to the power of 3432948736 ends in the digits 3432948736. This is a member of a sequence (Sloane's A121319) that is thought to be endless. It has the nice property that each member of the sequence adds a digit to the previous one. For example, 28736 ends in 8736, 248736 ends in 48736, 2948736 ends in 948736, and so on.
The only 10-digit pandigital polydivisible number in base 10: For each n from 1 to 10, the first n digits of this number, taken as an n-digit number, are divisible by n. For example, the first 3 digits are 381, and 381 is divisible by 3. The whole thing is divisible by 10 since it ends in 0, and any permutation of the 10 digits would be divisible by 9 since the sum the 9 digits is 45 which is a multiple of 9. But the other divisibility requirements impose tight constraints. See 381654729 for more about the pattern in these digits. See also 6210001000, 30000600003, 3608528850368400786036725, and 101.845773452536×1025.
This is 6403202/96 and appears in the Chudnovsky series approximation of pi.
4292853750 = 111111111101111110111111111101102
The Human population of the Earth according to the Arecibo message, which was transmitted in 1974. A more modern estimate is 6771000000. This is possibly the most dangerous number anyone has ever sent in any communication, because as Cassiday notes77, "Aliens who correctly interpret this will know how large an army to send".
See also 4294441822.
4294441822 = 111111111111011111111011010111102
Number of base-pairs in the Human genome, as given77 by the Arecibo message. A more modern estimate is 5941000000.
See also 4292853750.
The theoretical number of 32-bit IP addresses; the actual number is a few percent lower because some values are reserved for special purposes. See also 281474976710656.
First composite Fermat number. See here for more on these numbers; see also 17, 257, 641, (2222+1).
The number of years in the Hindu manvantara or "day of Brahma". See 1260 and 622080000000000.
This is e④π, where ④ is the higher-valued form of the hyper4 operator, using my (somewhat arbitrary and speculative) generalisation of tetration to real arguments based on the error function erf(x)). See also eπ, 4979.003621... and 11058015.34616.
(10-digit Armstrong number)
This number is equal to the sum of the 10th powers of each of its digits, and is unique in being the only 10-digit number to meet this requirement. Such numbers are called Armstrong numbers, Plus Perfect numbers, or narcissistic numbers. See also 153, 1634, 3816547290, 6210001000, and 115132219018763992565095597973971522401.
(base-pairs in the Human Genome)
The number of base-pairs in a haploid human genome counting 46 chromosomes (23 from each parent) and assuming that there is one X and one Y chromosome (i.e. a male individual).
See also 3.98×106020, 8.6×104515449, and 3.01607×103576838408.
The "self-describing number" described by Numberphile's James Grime in the video Maths Puzzle: The self descriptive number. It is the unique ten-digit number in which the first digit (6) tells how many zeros the number has; the second digit (2) tells how many 1's, etc., viz.:
The digits in 6210001000 comprise 6 zeros, 2 ones, 1 two, 0 threes, 0 fours, 0 fives, 1 six, 0 sevens, 0 eights, and 0 nines."
One might think that searching for such a number would require checking all 9,000,000,000 ten-digit numbers; but that's not needed because the digits must sum up to 10. As James mentions in the solution video, the search can be reduced even further by realising any solution must be one of the partitions of 10, of which there are only 42.
6210001000 isn't entirely unique in this regard: there are self-describing numbers with fewer digits: 1210, 2020, 21200, 3211000, 42101000, and 521001000.
Even more exotic is the "amicable pair" of 10-digit numbers: 6300000100 and 7101001000, found by Katie Steckles. Each describes the other.
See also 1026753849, 3816547290, and 4679307774.
13 factorial, the number of ways to rearrange 13 distinguishable objects. This number appears in some playing-card probabilities, such as 635013559600 and 2.235197...×1027. See also 1716.
Because 13 is 2×7-1, 13! is the magic constant for this "multiplicative" 7×7 magic square:
|
which is built on the principle of doing an elementwise multiplication (Hadamard product) on the following two components:
|
both of which satisfy the row, column, and diagonal requirements, but with repeated numbers. Is is quite efficient, in the sense that it uses 53.8% of the numbers from 1 to 7×13=91, or 67% of those that remain after casting out all primes greater than 13.
Similarly to the "self-describing number" 6210001000, this number's digits describe the digits in 7101001000, whose digits similarly describe the digits in this number. (Found by Katie Steckles).
This is 29 primorial, 2×3×5×7×11×13×17×19×23×29 and has a really easy-to-remember digit pattern: 646 969 323 0. The pattern results from the properties of 1001=7×11×13 and 2001=3×667=3×23×29, which multiplied together give 2003001, and 323=17×19.
(world population in 2009)
World population as of 2009 July 16th, as estimated by the U.S. Census Bureau, from the Wikipedia page. Another somewhat higher estimate is given by this site.
See also 1014.
Similarly to the "self-describing number" 6210001000, this number's digits describe the digits in 6300000100, whose digits similarly describe the digits in this number. (Found by Katie Steckles).
The first 10-digit prime number that appears as 10 consecutive digits of e:
e = 2.7182818284 5904523536 0287471352 6624977572 4709369995 9574966967 6277240766 3035354759 4571382178 5251664274 2746639193 2003050353 5475945713 8217852516 6427427466 ...
This is the answer to a puzzle that appeared on billboards in 2004. The billboards stated:
{first 10 digit prime in consecutive digits of e} . com
This little bit of nerd sniping led the solver to another, harder puzzle also involving digits of e. That puzzle, if solved, brought the user to a website soliciting resumes, potentially resulting in a call from someone at Google.
See also 9128219.
Alternate answer to the "first prime number in alphabetical order" question (see 8018018851).
This is the first prime number in alphabetical order in the English language: "eight billion eighteen million eighteen thousand eight hundred and fifty-one". It was found by Donald Knuth. All other numbers that occur earlier in alphabetical order (like 8 and 8018018881) are composite. ([154] p. 15 footnote)
Neil Copeland has suggested32 that 8000000081 is the alphabetically first prime, based on the spelling "eight billion and eighty-one". The use of and is common outside the U.S. (I have confirmed reports from the UK and New Zealand). Knuth, consistent with his statement in [149], does not use and.
See also 2.000...×1063 and 2.135987...×1096.
The sixth perfect number. The even perfect numbers (it is not known if there are any odd perfect numbers) can all be expressed in the forms:
2P-1 (2P - 1)
2N (2N+1 - 1)
where P is a prime and N = P+1. In this example, P is 17. Also, for the number to be perfect, 2P-1 must be prime, and is called a Mersenne prime. See here for a complete list of known perfect numbers.
See also the largest known perfect number.
Years in the Hindu "Day of Brahma" (see 622080000000000).
As discovered and described by Marius A. Burtea, this number is one of an infinite class of numbers that are both triangular and have the property of that any digit can be "moved to the denominator" and the result is an integer (see 742). The triangular construction begins with a number n of the form 10(b+2) + (10b-1)*100/3 + 27. In this example b=3 and n=133327; it is always a 1 followed by b 3's followed by 27. Then we can make the triaigular number n(n+1)/2 which always comes out to (b+1) 8's followed by (b+1) 1's followed by 28. Any number ending in 128 is divisible by 8 (because 128 and 1000 are both divisible by 8), and the same is true for anything ending in 112, and you always get an even number when removing just one digit, so that makes it satisfy the "742" property. Burtea also found two other infinite classes of numbers like this.
This is "Coulomb's constant", also called the "electric force constant" or "electrostatic constant", and is c2/107 N/A2 where c is the speed of light in metres per second, N and A are the units newton and ampere. Since c is defined to be precisely 299792458, Coulomb's_constant is precisely 8987551787.3681764 N m2/(A2s2); the units are equivalent to metres per farad.
(length of a second in Caesium-133 units)
Frequency (in Hz) of microwave radiation used as the basis of the Caesium-133 atomic clock. This number is part of the official definition of the second (the basic unit of time). The atomic clock technology was developed in the early 1950's and this number was adopted in 1967, with the wording "The second is the duration of 9,192,631,770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium-133 atom." As of 1st May 2019, the wording was changed but the number stayed the same.
The length of the second is originally derived from the rotation of the Earth and time-division decisions by the Babylonians, among other things (see 86400). It was recognized during the 18th century that the rotation rate of the Earth keeps changing. For example, using the period during 1750-1820 to define the average speed of Earth's rotation, and defining the second based on that, atomic clocks would be about 60 or 70 seconds out of sync with the Earth after another 100 years49. This is about enough to account for a variation of about 100 in this number 9192631770, depending on when and how the "standard second" is/was defined. Similarly, the number 299792458 that was for many years used to define the meter in terms of the speed of light would vary by about 2 or 3.
In 2019 the International System of Units (SI) was updated to define its seven base units in a way that defines all seven of them in terms of observable properties of nature, which are given arbitrary numerical values in terms of the base units. As mentioned above, the second had already been defined this way (i.e. arbitrary unit second is defined in terms of a natural phenomenon of Caesium-133). For an example of one that changed, see 1.602...×10-19.
Ten billion. This number appears in a Schoolhouse Rock! song; see 101010. See also 525600, 8675309, 1011, 0118 999 881 999 119 725 3, and 101010.
The upper limit of certain slide rule LL scales; see 22026.465794806.
A "pandigital" number (has all ten of the digits at least once) and the lowest such number that is prime. It is not possible to make a 10-digit pandigital prime because the sum of the first 10 digits is 45, and thus any such 10-digit number is a multiple of 9. See also 7652413. (From Pat Ballew[242] and @j0m0 on Twitter, who provided an complete list of 11-digit solutions)
The largest number that can be formed from the digits 1, 2 and 3 using the ordinary functions addition, multiplication and/or exponents. It slightly edges out 231=2147483648 because log(3)/log(2) is greater than 31/21. The next number in this sequence is 101.0979×1019.
First page . . . Back to page 15 . . . Forward to page 17 . . . Last page (page 25)
Quick index: if you're looking for a specific number, start with whichever of these is closest: 0.065988... 1 1.618033... 3.141592... 4 12 16 21 24 29 39 46 52 64 68 89 107 137.03599... 158 231 256 365 616 714 1024 1729 4181 10080 45360 262144 1969920 73939133 4294967297 5×1011 1018 5.4×1027 1040 5.21...×1078 1.29...×10865 1040000 109152051 101036 101010100 — — footnotes Also, check out my large numbers and integer sequences pages.
 s.30
s.30