Delta Hausdorff Dimension

Robert P. Munafo, 2010 Sep 7.

The box-counting dimension for a given neighborhood of a point, which is considered to be a term in a series, the limit of which would be the Hausdorff dimension.

It gives a rough qualitative estimate of the "apparent" Hausdorff dimension of an image at a given pixel resolution, and is computed by the following formula:

D_dh = log₂(POP_2s / POP_s)

Here D_dh represents delta Hausdorff dimension, POP_2s is the population (pixel count) on a pixel grid of size 2s, and POP_s is the population on a grid of size s. Both pixel grids cover the same area (as expressed in real and imaginary coordinates) but the second grid has twice as many pixels (sample-points).

If P is a point in the Mandelbrot Set, D_dh for a neighborhood of P is constrained to be in the range containing the Hausdorff dimensions of the Julia Sets for all points within the neighborhood. There are points in the Mandelbrot Set for which the Julia Set has a Hausdorff dimension "arbitrarily close" to 2.0. Since all neighborhoods of P contain embedded copies of the Mandelbrot Set, the upper bound of the range for any neighborhood is 2.0. As you zoom in, the neighborhood gets smaller and the lower bound of the range can go up. However the lower bound does not always go up. Also, the D_dh of the neighborhood can go up or down as you zoom in.

This is all sort of abstract, so I'll give some examples. To appreciate what's going on, compare the images to the numbers below. The number gives the fractal dimension of the image by the box-counting method; it can be anything from 1.00 to 2.00. The images were created using the distance estimator method.

In the first example, we're zooming in to the tip of a filament and D_dh goes down and reaches an asymptote quickly:

coordinates
0.00000 +1.00000i	radius 0.3 D_dh = 1.540	radius 0.1 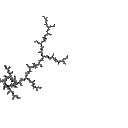D_dh = 1.349	radius 0.03 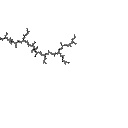D_dh = 1.255	radius 0.01 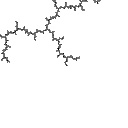D_dh = 1.238
	radius 0.003 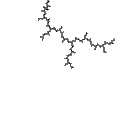D_dh = 1.278	radius 0.001 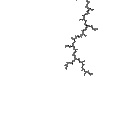D_dh = 1.248	radius 0.0003 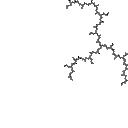D_dh = 1.278	radius 0.0001 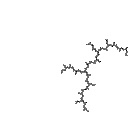D_dh = 1.257

In the second example D_dh goes up steadily as we zoom in, which is the most common behavior for most points that people usually zoom in to:

coordinates
-1.74856 +0.00075i	radius 0.3 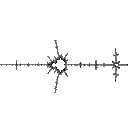D_dh = 1.275	radius 0.1 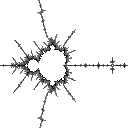D_dh = 1.389	radius 0.03 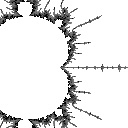D_dh = 1.547	radius 0.01 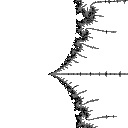D_dh = 1.548
	radius 0.003 D_dh = 1.594	radius 0.001 D_dh = 1.663	radius 0.0003 D_dh = 1.706	radius 0.0001 D_dh = 1.765

In the third example D_dh goes up and then goes back down:

coordinates
-1.74831	+0.00046i	radius 0.3 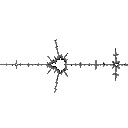D_dh = 1.361	radius 0.1 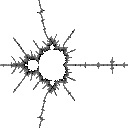D_dh = 1.400	radius 0.03 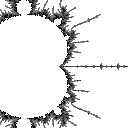D_dh = 1.568	radius 0.01 D_dh = 1.602
	radius 0.003 D_dh = 1.583	radius 0.001 D_dh = 1.602	radius 0.0003 D_dh = 1.357	radius 0.0001 D_dh = 1.382

It can occur that D_dh goes up and down several or many times, but you have to be willing to zoom in a really long way to see this happen. One example is the point

-1.769 110 375 463 767 385 + 0.009 020 388 228 023 440 i

if you zoom in "all the way" on these coordinates you see this:

the Munafo minibrot

References

The Wikipedia page on box-counting dimension is here: Minkowski-Bouligand dimension

Mu-ency main page — index — recent changes — DEMZ

This page was written in the "embarrassingly readable" markup language RHTF, and was last updated on 2023 Jul 03.

s.27