Feigenbaum Point
Robert P. Munafo, 2023 Aug 4.
The point R2{.1/2}x~ , located at approximately -1.4011551890920506... on the real axis (see Sloane's sequence A218453 for more digits). It is the limit of the main period doubling bifurcation sequence:
R2a, R2.1/2a, R2.1/2.1/2a, R2.1/2.1/2.1/2a,
R2.1/2.1/2.1/2.1/2a, R2{.1/2}x5a, R2{.1/2}x6a, ...
(pictures of all of these are below)
It is also the eastmost limit of the region of chaotic behavior of iterates on the real axis; and it is also the eastmost limit of islands on the real axis.
In the first sense (limit of the period-2, 4, 8, 16, ... mu-atoms) the point is called the Myrberg point, because P.J. Myrberg identified p=-1.401155... as the limit of the period-doubling cascade for the iteration z0 = 0 ; zn+1 = 1 + p zn2 in a 1962 paper [PM1] and with more digits (1.401155189) in the 1963 paper [PM2]; the misspelling "Myreberg" was introduced by Michael Barnsley. The result was rediscovered by Feigenbaum in 1978.
Generalised Feigenbaum Points
This particular point is just the most prominent of an infinite class of generalised Feigenbaum points. For any mu-unit U one can treat that mu-unit as the entire Mandelbrot set and then find with mu-unit within it corresponding to U; then do the same thing again, and so on.
R2, R2.1/3, R2.1/3.1/3, R2{.1/3}x3, ...
R2, R2.1/2.1/3, R2.1/2.1/3.1/2.1/3, R2{.1/2.1/3}x3, ...
R2, R2F(1/3B1)S, R2F(1/3B1)SF(1/3B1)S, R2{F(1/3B1)S}x3, ...
As one zoome in to any of these the density of filaments increases rapidly, similarly to an Osgood curve.
Illustrations
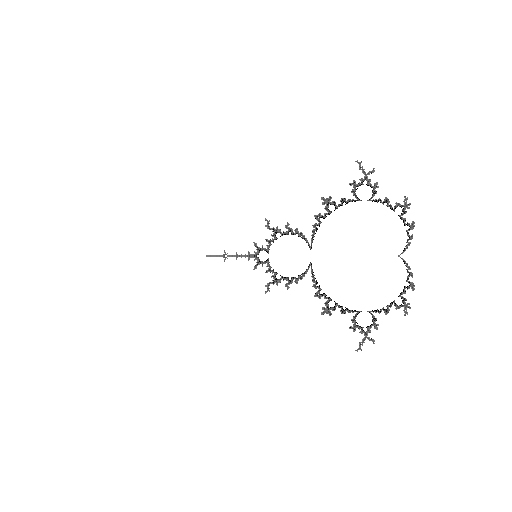
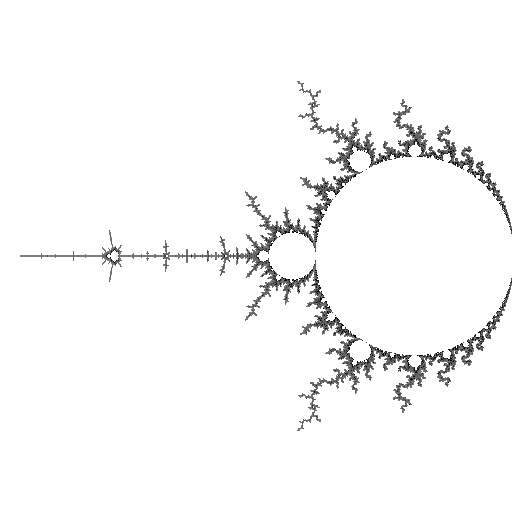
In the following sequence of illustrations, each view is centered at the Feigenbaum point and the magnification increases by 4.6692 (the Feigenbaum Constant) each time. The filaments become steadily denser until they fill the view.
(If you like the ASCII art, there is more at Cusp, Embedded Julia set, 2-fold Embedded Julia set, Paramecia, R2.C(0), R2.C(1/3), R2.1/2.C(1/2), R2t series, Seahorse Valley, and Reverse Bifurcation.)
 -1.401 +0.000i @ +6.034 | v_, :/~_ m-_-~--'\e.a, . _ -r` '(. ,.$~"--,` ]^ --,.,e)%` ' R2a --` ~^\____-, 'e :'^"^ \e .a" ]L-.,,.__/-T- /_.\ ' d"- |
 -1.401 +0i @ +1.292 | , ^m` ., -'e_,:, (e`_ ., ^'"d$a,.__"Y.'C,_ -"@,'""^^`'^^`"*e, , --_er"` ^*b 'b_ . -v/- '\ , , _-Yr/-m7" ` ._________~e____m_____d_edm*` ' R2.1/2a '^` " ' - `L"",__.a, , .""T""]c _- /" .`$-, ../ ~`^^Tb- , .a,r" '"@._Fvmvc:v-dF@`` .c:)*F' '.L@F`'F ^/; ` '\- r~` |
 -1.4011 +0i +0.2768 | .__/`,_, __ '`-^$^_ . '*c '^"/C . -d$ `"e_.~ "L , , , -TF- :c -_@)`, 'F ` '^'^bLee:L.c."\bm)/db,.a ^d'-%@**d/)@@`Y)m*@@L,- , -e- 'm,_'^*^b_-^` '`*Ym; ./-` '"\,. . '*"d"F^ '` -Y, , -*ba/L."v@" , , _-) _ (` -,,-_(Y/F""$[ _/_a_/__dm*\L_a_/e_L__$_edF*` ' R2.1/2.1/2a ( ' ' `-'$*L`' ]-``'`/``$Y@c___a, (period 4) ` .F ' ~` './F"@~""L .'@- .^FC -~ -^$r_ , /^ :.r` ad*"7YYm_ ..a[ -` '^ --"d@._m_,,,.___:_ed@"- m__am@d@F(^*@m@"$bF*['` ''-"(F``"'F'`:mF*"^'^F ^ .dCC` '` ']@"- 'F , ,_-"' " -b '-v"` 'T- _, -/._r"\, -*` "- |
 -1.40114 +0i @ +0.05929 | ,,..'$@^,_/" ^*L '^-vb '^"^^^"'*F@"__ . _/@e/ -'" ._"""@C\. ,F , '%@@-` (, -_, ^ _$bb@^,.v,-,^@ea_-.b- ^ 'L,, .____%@@^a.@ce'@@CL/:dCv.[ - '-"e, 'me, '^%7@F@@@@@/_@@*@C@@ddF.c '^\, '"._: '-_.,-m$d@`^T**^^`^^^-**@@L '@)_" -"*be . ^""@(mdF"` '" ., ^^"YL- 'c .,'.T@@)^e/C@@^` "\. :, ^"@_ac vb-.'~a-:'@bb@@m@` _v.//..\,dmdYdL::$r]e\@dm$@@`` '" R2.1/2.1/2.1/2a ^7"^F^"@^"$\m@"T^@(T"F@@F@bm, .. (period 8) .d' '` ^d$'^- -@`'._*'-%d@@@m@@c '' ._%@@- .` '`_:'@@``F'(@b- -a""_ -v(bC'' :.$YYF@b__ _. _aa`` __-^T a-"`;-vY@;_:e_,_ ___:_emdF .__F" .a/` ,/-\m@@@b@@TFF@e@@@dFFF'[ ./^- --^""@@@"Y"@`F'd@@*F'YF~'C`- ' ,.-vmF@^-'$`'~~@F\' *F\ `_: '-._^mF^" 'C -d@_ :[ -~` ._,e_a,-_d@"^- " ^^@F\ ' _.\ '^` "^Y@F"^`, _a` __a(@ |
 -1.40115 +0i @ +0.01269 | -_e,,_-,,-.d@@C7e)"^ a '^^@,,_r ''""m@ mr ' ^^^^"Y"$"7Y@@@Ce- ./. '-_'@m@% 'r_'`'^* :@m. .__aa*FY@@eac_@. c '$@@m^,'(/.'-a' '"_, :e ,_ '` ` -^dd@@@@%/'@.:((@(d\Tm@".,^^ '^\Lm` '"e_ _ '--aa__%@@@$/d@;bF@@@@@a@@r.@,~ --"~*ea~ _/d(_, , ``'(^$F@@@@@@@dd@@*Y@@@@@@Lb -"C@/. :- -^*Led-/`m_e,vd@@@[^T**^^ ^`^'"*@@b _, .,.-@ba/- 'e --~@@d,)//*Y@@d@F"` '" 'La '"**@@a~_'dm -_/^%Y@@b@md@@@^ .''@L ),^^F@C_Cd(bd.^@a-CF@@@@@@@` \bd/@a_bL$b@Y@$/m@bdLd@@@@@@`` '" R2.{1/2}x4a *@"@@*Y@FY@bm@@@Y@@@FF@@@@bm, .. (period 16) `'@^ /"-^.@F"/'"@L'\/Y((@@@@@b@@c a/^ _.%$@@ve'.:@ .~"-$^@@YT@@Y@b- "` '^'_/F*b, -/ _"-d@@"@`%_@@@@@b_, .. -__:mF` ]c .,_/FT,\.aFFL%@@@@;_:____ ___.__md@ .___dF*_ '$d@*` ".'`-,/mdd@@@b@@@@@@_d@@m@@@FF .:d*b- ._r^ ' ./-Y*Y*@@@@"YT@F@7@@@@@Y@@Y'@-\ __"- ') '` _ ,-__$mm@$@$\'@))~T@@Y".F@L'"a: dmd` ^^-)ee$@FF*`"@;'F -v@@e,`.m['.,"^ FL . ,_.^_a,-,-%@@(F-_ -Y` :/*"@FL' ./' __:\ -"r^^^^^"^*YY@C"FC__ * _./F``[ -,_m@@ |
 -1.401155 +0i @ 0.002719 | ,-- ^*-r(ea,:m_,(d$@@@@d@*"^:/, ^^"@C)/) .^""Y@@@ b@,.c -^^^""@*@"@*@@@@@CmF,e$_."\C@@@@\;'@.^"Y$F (@bL_ ], _ '^^d`/_mdF@@@@Lm\$@L-L/C@@@@"a'@@-'bmC `'**_a,.L- '-_:. ^^"^-`"-CC@@@@@@b/@L\@@@@dC]@@d(c*@ _,:'@@bdF_a ''@dcde.^-\e)mad@@@@@@@@@b@@@@@@d@@b%@)\ '^)"YY@@)d` : ._$@@a\-_^^^*@@@@@@@@@@@@@@@*Y@@@@@@b@ _ ---"@@/L.]c .'~"@*bL@cF"@me/@@@@@[^T**^^ ^`^'^*@@@ /ec -.,:(@bd@-,-d.`-v@@@@b@[@@@@@@@F"` '" .'@_c:'"*Y@@bF.\@de~e/^C@@@@@b@@@@^ :'"@//@a($@@@b@]d@d:T@m/@@@@@@@@@` eb/@@@d@b@@@Y@@@@@@@@@@@@@@@`` '" R2.{1/2}x5a F@F@@@@@@@@bm@@@@@@@@@@@@@bm, .. (period 32) -^$@F"dY~*@@@@@^@@@T$@@@@@@@@@m@@c .\d"/-^.$@@@\b":/@-:F(\@@@@@@@@@@b- $FF -""%$@@Y@(-ad`_):m@@@@@\C@@@@@@b_, _. " .-e%b@@"'$m "_v_a$FF@F`\mFFC@@@@@^.:e___ ___.__md@ ._eeaa@@@(^ : -'\@@Y^.*d~^%ad@@@@@@b@@@@@@_d@@m@@@@@ "`'_\@F@"'\ ._mm"^F `:arYYY*@@@@@@@@@@@@@@@@@@@@*@Y) .v_a*(`'@- a_"T' __,,.`-e.mb@@@@@YY@7b@@@@@7:@@CF"-b %m@^- .` ^ __.^^"Tm@L(@@@@@FY@):@\vd@@b(\.d@/\a@* @C`^- ._-,,.$eb(dCm@@@@@F_`7Y~~\@*Y@@@%`\@".%_m@ `^c ___v"FY"^$""%*@@@@Y@@)e`'Y`.^-\dF"^b`"'.L)@@@ |
 -1.4011551 +0i @ 0.0005823 | ,]) _ "^*-mdmba%bmL@@@@@@@@@@F%-@/'7Y@@@)m@`m***@@@@ @@/:C -_ ---"7"*Y@@@@@@@@@@@@b@LL@L[*b@@@@@@)@@/TF@@@ @@@C_--]m '\a_^'^":`dm@@@@@@@@@@@@C)@F@@@@@@@@@@e"@@@ ^(YYdd.(@/.^"*_ba/^""""^**@@@@@@@@@@@@@@@@@@@@@@@@d@@ a,_"@@bdF\d-/-@@@e/Lc^"bm@bd@@@@@@@@@@@@@@@@@@@@@@@@@ ^%FF@@@@b@\`(c-/_@@@bL\/^@7Y@@@@@@@@@@@@@@@*Y@@@@@@@@ a,--(F*@@@@.@F/e"*F@@@b@CFY@@@@@@@@@[^T**^^ ^^^'""Y@@ $b)/v(CY@@@@@F)(@\^b@@@@@@@@@@@@@@@F" '" .$@ec(^@@@@@@@$Y@@bYd$@@@@@@@@@@@@'` :7Y@@(@m@@@@@@@d@@@@@@@@@@@@@@@@@` @@@@@@@@@@@@@@@@@@@@@@@@@@@@`` '" R2.{1/2}x6a @@@@@@@@@@@bm@@@@@@@@@@@@@bm, .. (period 64) T^@@@C@@@@@@@@@@@@@@@@@@@@@@@bm@@c '%@*F/^d@@@@@@$]@@(TF@@@@@@@@@@@@b- -FC-aF*$@@@@@@"b@F_)b@@@@@@@@@@@@@@m_, _. Y`Le_dC@@@*7@b`/^(bm@@@@@F@@@@@@@@@@;.:____ ___.__md@ ./mmad@@@@%-d[.-d@@@@@%*-Y$@@@@@@@@@b@@@@@@_d@@m@@@@@ *""d@@@@F^b-^.ad@FYF`\bm@@@@@@@@@@@@@@@@@@@@@@@@@@@@@ --adFY"/@Y'..m*Y".'`%^_F(L/@@@@@@@@@@@@@@@@@@@@@@@F$@ @@@@",-:( .-"'_L,%^"*@@@@@@@@@@@@@@]@@@@@@@@@Y@@F@@@@ @@F"r -" -,__m_d%@bbC@@@@@@@@@@FF@*^)@F@@@@@\T@Ya%)d@ `$b ^ -_a__(@F@*T@@F@@@@@@@@@@@):@Y-(b@@@YY@`/^d@$@@@ |
 -1.4011552 +0i @ 0.0001247 | dd@Lm'-*@YYb@@@m$@@@@@@@@@@@@@@C/@@Y@@@@@@@@Fd@@@@@@@ @@@a@-~_:--/Y@YY@@@@@@@@@@@@@@@@@@@C@@@@@@@@b@@d@@@@@ @@@@m/-@d,~m/.Y'YY@^@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@ %@@@@dCd@m:^*Ydba^C*F"*@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@ m;$@@@@@@Cdcdd@@@d@@dF@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@ ^$@@@@@@@@@L@)v@@@@@@b@@@@@@@@@@@@@@@@@@@@@*Y@@@@@@@@ d,-mY@@@@@@@@@/dYY@@@@@@@@@@@@@@@@@@`^T**^^ ^`^'^*@@@ @@@(d@@@@@@@@@b@@@@@@@@@@@@@@@@@@@@F"` '" ]@@@b@@@@@@@@@@@@@@@@@@@@@@@@@@@@@'` m@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@` @@@@@@@@@@@@Y@@@@@@@@@@@@@@@`` '" R2.{1/2}x7a @@@@@@@@@@@bm@@@@@@@@@@@@@bm, .. (period 128) @@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@c ($@@@F@@@@@@@@@@@@@@@@@@@@@@@@@@@b\ Y@@(@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@b_, _. @`)@m@@@@@@@@@;@%d@@@@@@@@@@@@@@@@@@^.:____ ___.__md@ amddd@@@@@@~@F%r@@@@@@@@@@@@@@@@@@@@b@@@@@@_d@@m@@@@@ F(C@@@@@@7@["Ldd@@Y@F%b@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@ :m/@@@@@@Y'`$mY@Y^C\$$%@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@ @@@@Y(\(@-.m*T_Ld$$@F@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@ @@FY)':*:aem%mm$@@@@@@@@@@@@@@@F@@@F@@@@@@@@@@@@@@@@@ *@@`7 ;_amb@@@@@Y@@@@@@@@@@@@@@@Y@@7C@@@@@@@[@Cd@@@@@ |
 -1.40115519 +0i @ 0.00002671 | @@@~b,"Y@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@ @@@@@LTm:-/@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@ @@@@@@)@@)\m@)@Y@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@ @@@@@@@@@@b$Y@@@dC@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@ dC@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@ Y@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@*Y@@@@@@@@ @CF@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@[^T**^^ ^^^'^"@@@ @@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@F"` '" @@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@` @@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@` @@@@@@@@@@@@@@@@@@@@@@@@@@@@`` '" R2.{1/2}x8a @@@@@@@@@@@bm@@@@@@@@@@@@@@m, _. (period 256) @@@@@@@@@@@@@@@@@@@@@@@@@@@@@bm@@e @@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@b- @@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@b_, .a @F@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@^_:e___ ___.__md@ dm@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@b@@@@@@_d@@m@@@@@ @Y@@@@@@@@@@@b@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@ bd@@@@@@@@$L@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@ @@@@@CY@@(T@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@ @@@@@(v@Tdbd@@b@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@ *@@[@\$edb@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@ |
revisions: 19960209 oldest on record; 20230328 add images, link to period doubling and chaos articles, make ASCII versions a bit smaller; 20230616 generalised Feigenbaum points; 20230702 give the coordinate to more digits; 20230804 link to OEIS; Myrberg point
From the Mandelbrot Set Glossary and Encyclopedia, by Robert Munafo, (c) 1987-2024.
Mu-ency main page — index — recent changes — DEMZ
This page was written in the "embarrassingly readable" markup language RHTF, and was last updated on 2023 Aug 07.
 s.27
s.27