Leavitt Navigation
Robert P. Munafo, 2023 Aug 9.
"Leavitt Navigation" is a method pioneered by Jonathan Leavitt and more recently referred to by more generic terms such as "morphing" (referring to the way that the shapes of embedded Julia sets are changed via the square root map into distorted or " morphed" shapes)
This is an example of how I typically locate a "morphed" image, provided I have a clear idea of its design (perhaps from an understanding of the self-squared and exponential mappings).
The technique uses some of the special features of Power MANDELZOOM. Here I will be finding a simple 3rd-order embedded Julia set (EJS) based on the pattern I call "X chromosomes".
We'll start with this view, which is centered at -1.76863 +0.00266 i, size = 0.00125:
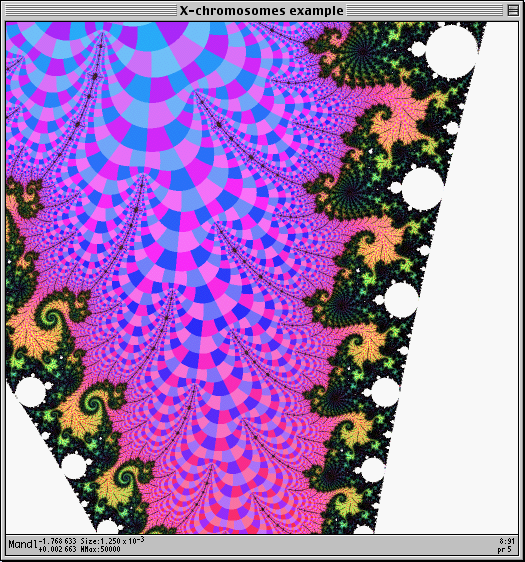
To get the chromosomes we need a free chain of the tip of a pointy 1st-order EJS. This involves zooming in for a while near the tip of this embedded Julia set:
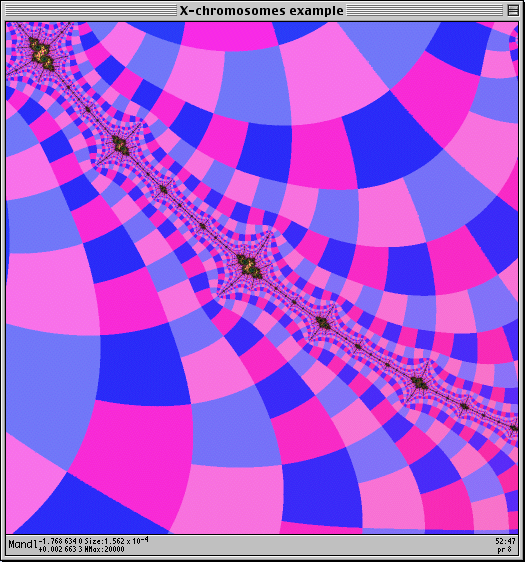
(Coordinates: -1.76863411 + 0.00266330 i, size = 0.0000195)
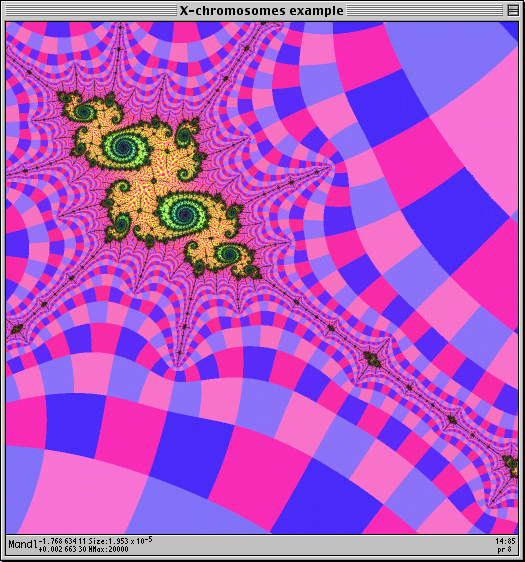
I zoom in close to its "tip" until I get to here:
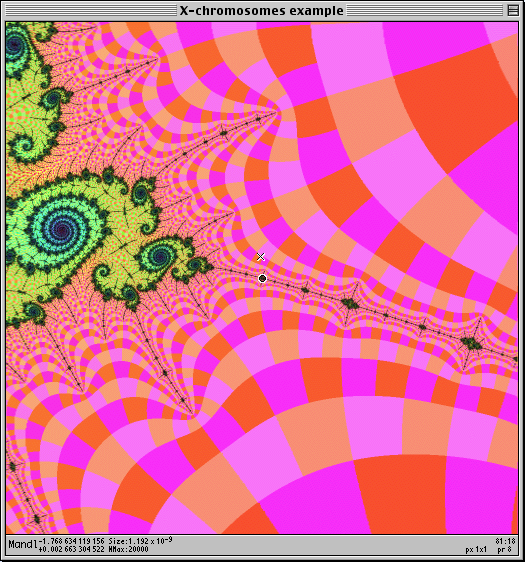
Then I just arbitrarily pick a tiny Julia set, which is going to be the first one I actually zoom in to the center of. The one I pick is near the "O" in the above image, just under the "X". Here is that EJS:
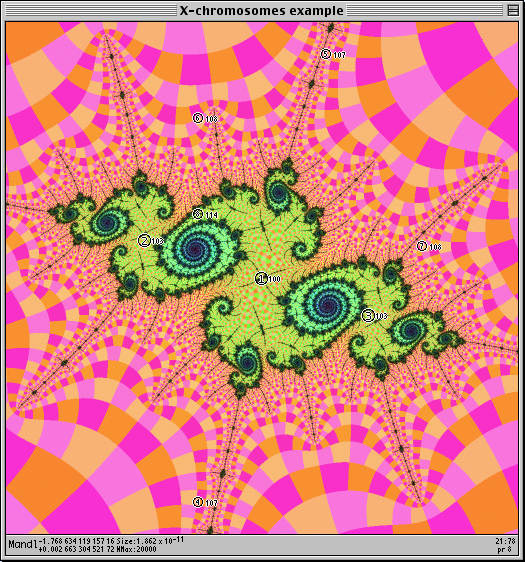
(Coordinates: -1.76863411915716 + 0.00266330452172 i, size =
1.9×10-11)
This is a second-order embedded Julia set, because it is influenced by two islands: the large period-3 island R2F(1/2B1)S, and this period-65 island, which is located at the center of the Julia set whose tip we were approaching during the previous few images. (We never saw the period-65 island because we never had it in the center of the view).
At this point I use the special period-finding command, which uses the algorithm described in the period article starting with the section titled "Finding the Period of a mu-Atom", and also described in the Jordan curve method article. It uses the Jordan Curve theorem to track the vertices of a polygon that starts as the rectangular boundary of the current view, iterating all vertices one step at a time until the resulting polygon contains the origin. The number of iterations performed is thus the period of a mu-atom somewhere inside the original polygon. It uses an inverse bilinear interpolation technique (described in the article inverse interpolation for a quadrilateral) to figure out approximately where in the window the center of the mu-atom is likely to be.
As you can see, it found a period 100, which is labeled with a large circled "1" in the center of the image because it is the lowest-period found. Next to the circled "1" is a tiny "100" indicating the period. My program also scans across the image trying little squares to locate more mu-atoms, and reports the lowest 9 periods it finds. It found some with periods 103, 104 and 105. As seen here, the positions are sometimes wildly inaccurate causing the numbers to be in the middle of wide dwell bands were clearly there are no filaments or islands.
After executing the "special period-finding command" I can then zoom in with a "Zoom to 1st Found Period" command (and there are similar commands for 2 through 9).
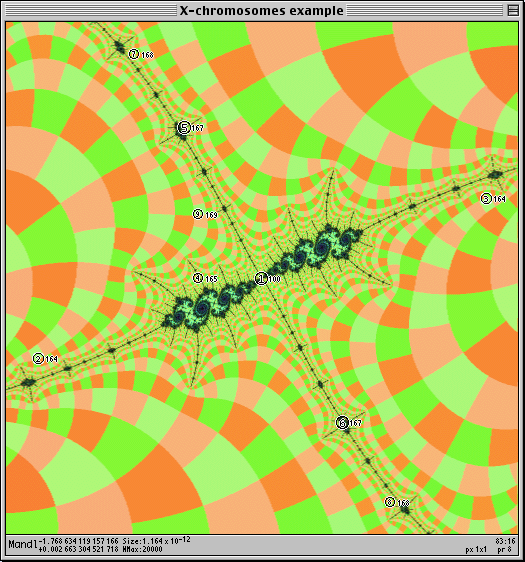
At periodic intervals I need to repeat the "find period" command because its calculation of the location of the period-100 is not exact. (As it turns out, the closer you zoom in, the more exact it is, because the precision of the linear interpolation depends on how far away the next lower period is located in relation to the size of the polygon, which is the same as the size of the current view. In this case we're zooming in towards a period-100, and the next-lower period is the owner of the nearby Julia set that you'll see if you look at -1.7686341190573 + 0.0026633044939 i, size 2×10-11. That is one of the Julia sets that I passed by on my way to this one).
I continue zooming on the center:


Until I get to this point:

(Coordinates: -1.76863411915716693095 + 0.00266330452171772597 i,
size = 7.1×10-17)
I want this large X shape to get distorted into an "X-chromosome", so I need to "go off-axis", i.e. select a new center for subsequent zooms. A doubled, distorted version of everything seen here will become part of the exponential map of the new center-point.
To get the desired "X" shape I have to pick a new zoom point near the "O" in the image, which you will find near the right edge (with a small "X" above it). There is a Julia set under that "O" but it's too small to see.
I zoom at that point manually until the Julia set fills the view, and then do "find period" again:
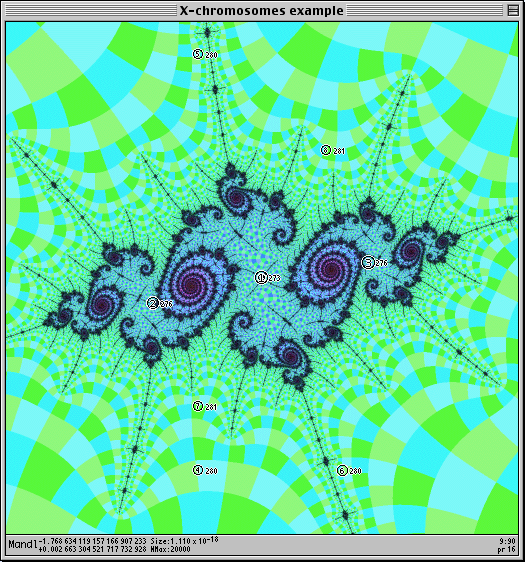
(Coordinates: -1.768634119157166907234 + 0.002663304521717732925 i,
size = 1×10-18)
Now I can zoom automatically again. As before, I continue to zoom in using the Find Period command every now and then to make sure it's centered.
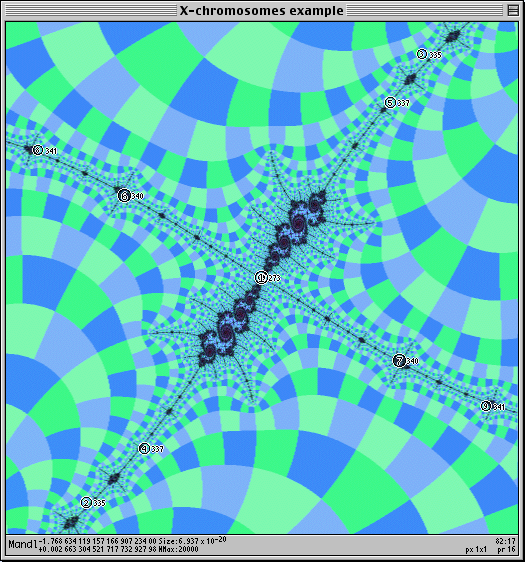
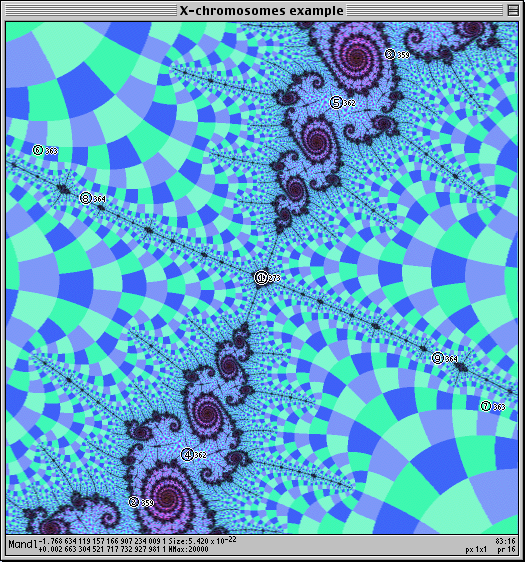


At this point we see the two "squared" copies of the X shape. I want four in a symmetrical circular arrangement, so I just continue:



The cell now has four "X" chromosomes. "Y" chromosomes are left as an exercise for the reader.
The coordinates of the final image are:
and it required 161-bit (triple-double) precision to draw the final image.
Here is an exponential map of the same zoom sequence:

|

|

|

|

|

|

|

|

|

|
|

|
|
Historical Note
I originally wrote this article for James W. Morris, prefacing it with this introduction in an email I sent on 2010 Dec13:
The period-detection command [in Power MANDELZOOM] is critical for finding Leavitt images. I have prepared an explanation of the basic technique I use as a web page, because I will probably add it to my Mu-Ency pages sometime. You can read it here: (link)
We communicated back and forth for quite some time developing techniques for choosing the time and place to change focus (center) while constructing a long zoom sequence. I also included Claude Heiland-Allen and Simon Hosie in the same discussions; and both created many Leavitt-like images of their own. This article and much of my work from that period remained buried at obscure URLs until 2023.
revisions: 20101213 original article written for James Morris; 20230620 moved to mu-ency and minor rewriting; 20230809 "morphing" name origin
From the Mandelbrot Set Glossary and Encyclopedia, by Robert Munafo, (c) 1987-2024.
Mu-ency main page — index — recent changes — DEMZ
This page was written in the "embarrassingly readable" markup language RHTF, and was last updated on 2023 Aug 09.
 s.27
s.27